The Open Group Base Specifications Issue 7, 2018 edition
IEEE Std 1003.1-2017 (Revision of IEEE Std 1003.1-2008)
Copyright © 2001-2018 IEEE and The Open GroupA newer edition of this document exists here
NAME
erf, erff, erfl - error functions
SYNOPSIS
#include <math.h>
double erf(double x);
float erff(float x);
long double erfl(long double x);
DESCRIPTION
[CX] ![[Option Start]](../images/opt-start.gif)
The functionality described on this reference page is aligned with the ISO C standard. Any conflict between the
requirements described here and the ISO C standard is unintentional. This volume of POSIX.1-2017 defers to the ISO C
standard.
![[Option End]](../images/opt-end.gif)
These functions shall compute the error function of their argument x, defined as:
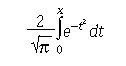
An application wishing to check for error situations should set errno to zero and call
feclearexcept(FE_ALL_EXCEPT) before calling these functions. On return, if errno is non-zero or
fetestexcept(FE_INVALID | FE_DIVBYZERO | FE_OVERFLOW | FE_UNDERFLOW) is non-zero, an error has occurred.
RETURN VALUE
Upon successful completion, these functions shall return the value of the error function.
[MX] ![[Option Start]](../images/opt-start.gif) If
x is NaN, a NaN shall be returned.
If
x is NaN, a NaN shall be returned.
If x is ±0, ±0 shall be returned.
If x is ±Inf, ±1 shall be returned. ![[Option End]](../images/opt-end.gif)
If the correct value would cause underflow, a range error may occur, and erf(), erff(), and erfl() shall
return an implementation-defined value no greater in magnitude than DBL_MIN, FLT_MIN, and LDBL_MIN, respectively.
[MXX] ![[Option Start]](../images/opt-start.gif) If the IEC 60559 Floating-Point option is supported, 2 * x/ sqrt(
If the IEC 60559 Floating-Point option is supported, 2 * x/ sqrt( ) should be
returned.
) should be
returned. ![[Option End]](../images/opt-end.gif)
ERRORS
These functions may fail if:
- Range Error
- [MX]
![[Option Start]](../images/opt-start.gif) The result underflows.
The result underflows.
If the integer expression (math_errhandling & MATH_ERRNO) is non-zero, then errno shall be set to [ERANGE]. If
the integer expression (math_errhandling & MATH_ERREXCEPT) is non-zero, then the underflow floating-point exception
shall be raised. ![[Option End]](../images/opt-end.gif)
The following sections are informative.
EXAMPLES
Computing the Probability for a Normal Variate
This example shows how to use erf() to compute the probability that a normal variate assumes a value in the range
[x1,x2] with x1<=x2.
This example uses the constant M_SQRT1_2 which is part of the XSI option.
#include <math.h>
double
Phi(const double x1, const double x2)
{
return ( erf(x2*M_SQRT1_2) - erf(x1*M_SQRT1_2) ) / 2;
}
APPLICATION USAGE
Underflow occurs when |x| < DBL_MIN * (sqrt( )/2).
)/2).
On error, the expressions (math_errhandling & MATH_ERRNO) and (math_errhandling & MATH_ERREXCEPT) are
independent of each other, but at least one of them must be non-zero.
RATIONALE
None.
FUTURE DIRECTIONS
None.
SEE ALSO
erfc, feclearexcept, fetestexcept, isnan
XBD Treatment of Error Conditions for Mathematical Functions, <math.h>
CHANGE HISTORY
First released in Issue 1. Derived from Issue 1 of the SVID.
Issue 5
The DESCRIPTION is updated to indicate how an application should check for an error. This text was previously published in the
APPLICATION USAGE section.
Issue 6
The erf() function is no longer marked as an extension.
The erfc() function is split out onto its own reference page.
The erff() and erfl() functions are added for alignment with the ISO/IEC 9899:1999 standard.
The DESCRIPTION, RETURN VALUE, ERRORS, and APPLICATION USAGE sections are revised to align with the ISO/IEC 9899:1999
standard.
IEC 60559:1989 standard floating-point extensions over the ISO/IEC 9899:1999 standard are marked.
IEEE Std 1003.1-2001/Cor 2-2004, item XSH/TC2/D6/22 is applied, adding the example to the EXAMPLES section.
Issue 7
POSIX.1-2008, Technical Corrigendum 1, XSH/TC1-2008/0092 [68] is applied.
End of informative text.
return to top of page
UNIX ® is a registered Trademark of The Open Group.
POSIX ™ is a Trademark of The IEEE.
Copyright © 2001-2018 IEEE and The Open Group, All Rights Reserved
[ Main Index | XBD | XSH | XCU | XRAT
]
![[Option Start]](../images/opt-start.gif) The functionality described on this reference page is aligned with the ISO C standard. Any conflict between the
requirements described here and the ISO C standard is unintentional. This volume of POSIX.1-2017 defers to the ISO C
standard.
The functionality described on this reference page is aligned with the ISO C standard. Any conflict between the
requirements described here and the ISO C standard is unintentional. This volume of POSIX.1-2017 defers to the ISO C
standard. ![[Option End]](../images/opt-end.gif)
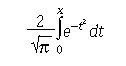
 ) should be
returned.
) should be
returned.