
B Relationships (Normative)
This appendix details the normative requirements for relationships between elements of the ArchiMate modeling language.
B.1 Specification of Derivation Rules
The following sections specify the formal rules for deriving relationships. The input relationships used for derivation must be allowed by the tables in this appendix. The resulting relationship will then always be allowed by definition and is listed in these tables as well. Note that these derivation rules do not work on relationships with grouping, or between core elements and other elements such as motivation, strategy, or implementation and migration elements, with the exception of the realization and influence relationships. This appendix states in more detail the restrictions that were applied to the use of the derivation rules to arrive at the relationship tables. Applying these rules and restrictions together results in the tables in this appendix, which contain all allowed relationships in the language.
We distinguish between two types of derivations: those that are certainly true in any model where these rules apply, and those that are potentially true but uncertain, depending on the specifics of the model concerned.
Notation of Derivation Rules
In the description of the derivation rules a shorthand is used to describe relations: p(a,b):R is used to describe the relationship with name p that has concept a as source, concept b as target, and R as its relationship type.
The source and target concepts may be of any type. The relationship type can be restricted by the definition.
By convention, concepts are named a, b, and c in order of appearance, relationships are named p, q, and r in order of appearance, and relationship types are named S, T, and U in order of appearance.
B.2 Derivation Rules for Valid Relationships
This section states the derivation rules for derivations that are valid in any model where these rules apply.
B.2.1 Valid Derivations for Specialization Relationships
If two relationships p(a,b):S and q(b,c):S exist, with S being Specialization, then a relationship r(a,c):S can be derived.

Example 37: Transitivity of Specialization
B.2.2 Valid Derivations for Structural Relationships
The structural relationships can be ordered by “strength”:
• Realization (weakest)
• Assignment
• Aggregation
• Composition (strongest)
Part of the language definition is an abstraction rule that states that two structural relationships that join at an intermediate element under specific conditions can be combined and replaced by the weaker of the two.
If two relationships p(a,b):S and q(b,c):T exist, with S and T being structural relationships, then a relationship r(a,c):U can be derived, with U being the weakest of S and T.

Example 38: Derivation of Structural Relationships
Informally, this means that if two structural relationship are “in line” (the target of one relation joins at the source of the other relation) they can be replaced by the weakest of the two. Transitively applying this property allows us to replace a “chain” of structural relationships that are in line (with intermediate model elements) by the weakest structural relationship in the chain.
An example is shown in Example 39: assume that the goal is to omit the functions, sub-functions, and services from the model. In this case, an indirect realization relationship (the relationship labeled “Derived Relationship” (thick arrow on the right) can be derived from “Financial Application” to the “Payment Service” (from the chain assignment – composition – realization).
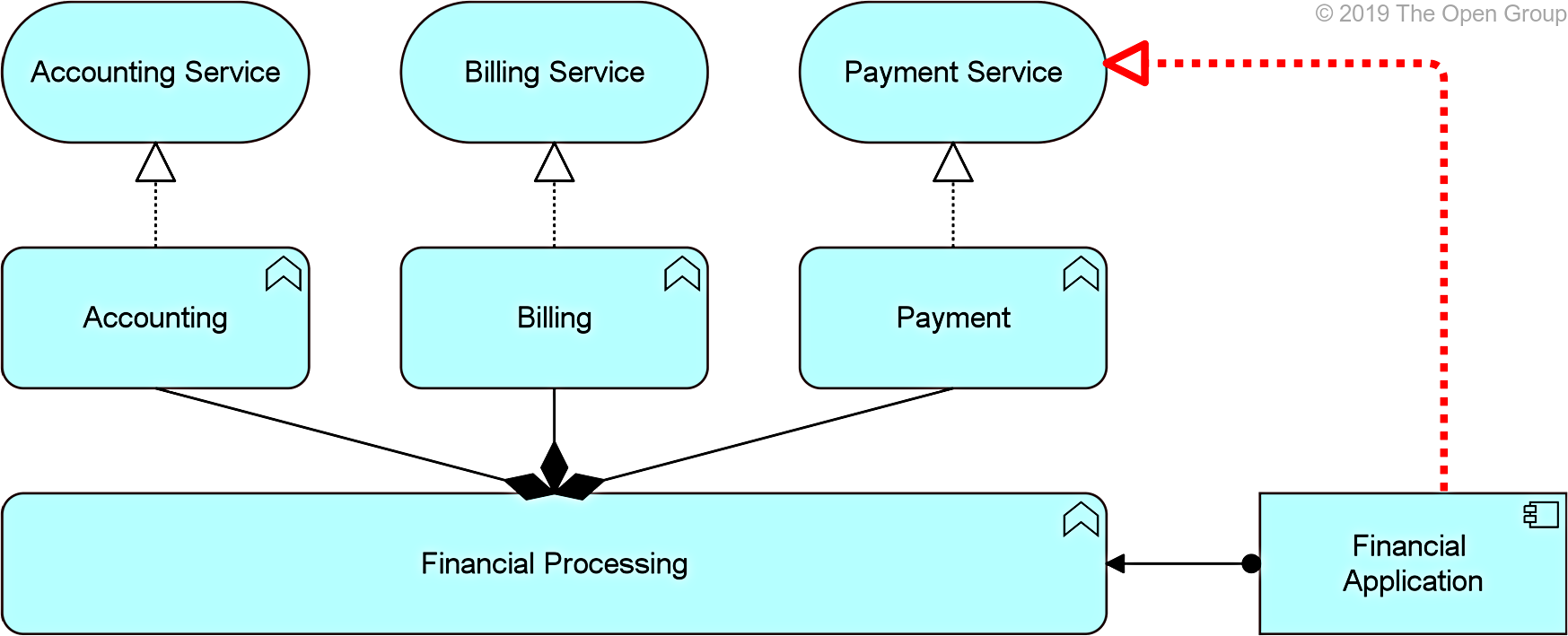
Example 39: Derivation from a Chain of Structural Relationships
B.2.3 Valid Derivations for Dependency Relationships
Part of the language definition is an abstraction rule that states that a structural relationship and a dependency relationship that join at an intermediate element under certain conditions can be combined and replaced by the dependency relationship. This rule is split into two parts for both the source and target side of the dependency.
If two relationships p(a,b):S and q(b,c):T exist, with S being a structural relationship and T being a dependency relationship, then a relationship r(a,c):T can be derived.
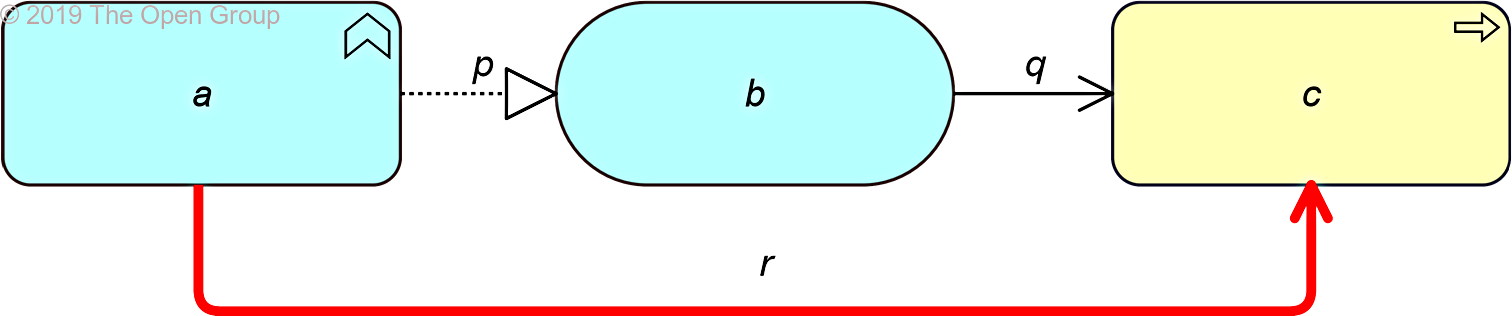
Example 40: Derivation from a Dependency and a Structural Relationship in Line
If two relationships p(a,b):S and q(c,b):T exist, with S being a structural relationship and T being a dependency relationship, then a relationship r(c,a):T can be derived.

Example 41: Derivation from a Dependency and a Structural Relationship in the Opposite Direction
These rules may be combined with the derivation rule for structural relations (DR2), allowing to replace a “chain” of structural relationships and a dependency relationship (with intermediate model elements) by the dependency relationship in the chain, given that the chain does satisfy the restrictions for structural and dependency relationships. Informally, this means that the begin and/or endpoint of a dependency relationship can be transferred “backwards” in a chain of elements connected by structural relationships.
B.2.4 Valid Derivations for Dynamic Relationships
Part of the language definition is an abstraction rule that states that a structural relationship and a dynamic relationship that join at an intermediate element under certain conditions can be combined and replaced by the dynamic relationship. This rule is split into a generic rule and rules specific for flow and triggering.
For the two dynamic relationships, the following rules apply.
If two relationships p(a,b):S and q(b,c):T exist, with S being a structural relationship and T being a dynamic relationship, then a relationship r(a,c):T can be derived.

Example 42: Derivation from a Dynamic and a Structural Relationship in Line
If two relationships p(a,b):S and q(c,b):T exist, with S being a structural relationship and T being Flow, then a relationship r(c,a):T can be derived.

Example 43: Derivation from a Flow and a Structural Relationship in the Opposite Direction
If two relationships p(a,b):S and q(b,c):T exist, with S being Triggering and T being a structural relationship, then a relationships r(a,c):S can be derived.
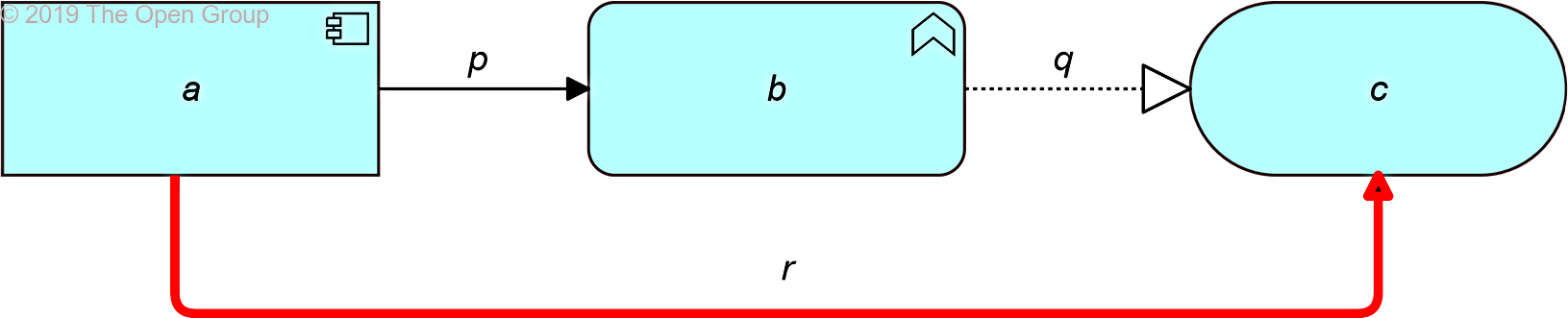
Example 44: Derivation from a Triggering and a Structural Relationship in Line
These rules can be applied repeatedly. Informally, this means that the begin and/or endpoint of a flow relationship can be transferred “backwards” in a chain of elements connected by structural relationships. Example 45 shows two of the possible flow relationships that can be derived with these rules, given a flow relationship between the two services.
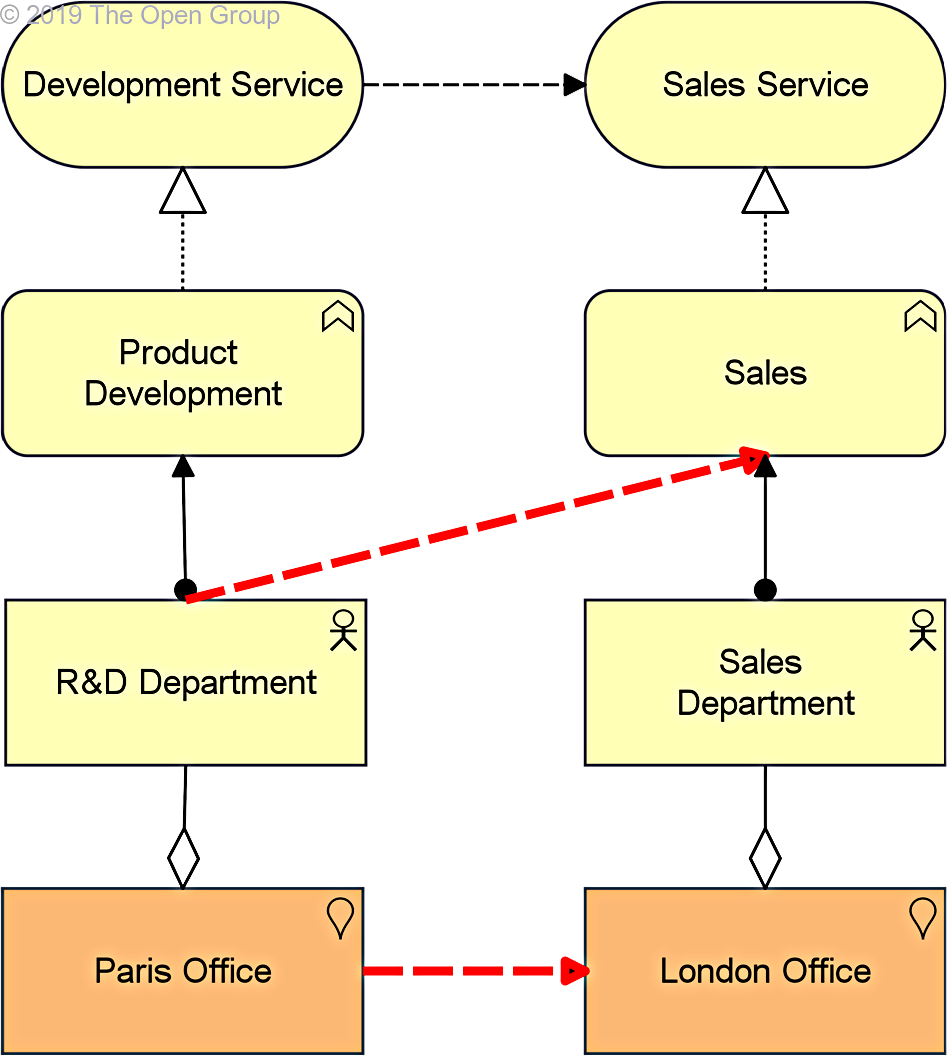
Example 45: Derivation from Dynamic Relationships
Moreover, triggering relationships are transitive, as expressed in the next rule.
If two relationships p(a,b):S and q(b,c):S exist, with S being Triggering, then a relationship r(a,c):S can be derived.

Example 46: Derivation from Triggering Relationships
This rule may be combined with the rules for deriving dynamic relations and structural relationships, thus allowing discovery of triggering relations. Example 47 shows how the “Sales Department” is assigned a business process “Selling” that triggers a business process “Invoicing”, which is composed of the business processes “Billing” and “Payment”. “Invoicing” in turn triggers the business process “Shipping” that is assigned to the “Shipping Department”. The derivation rules allow that the “Sales Department” triggers the “Shipping” business process, but also the business process “Billing”.
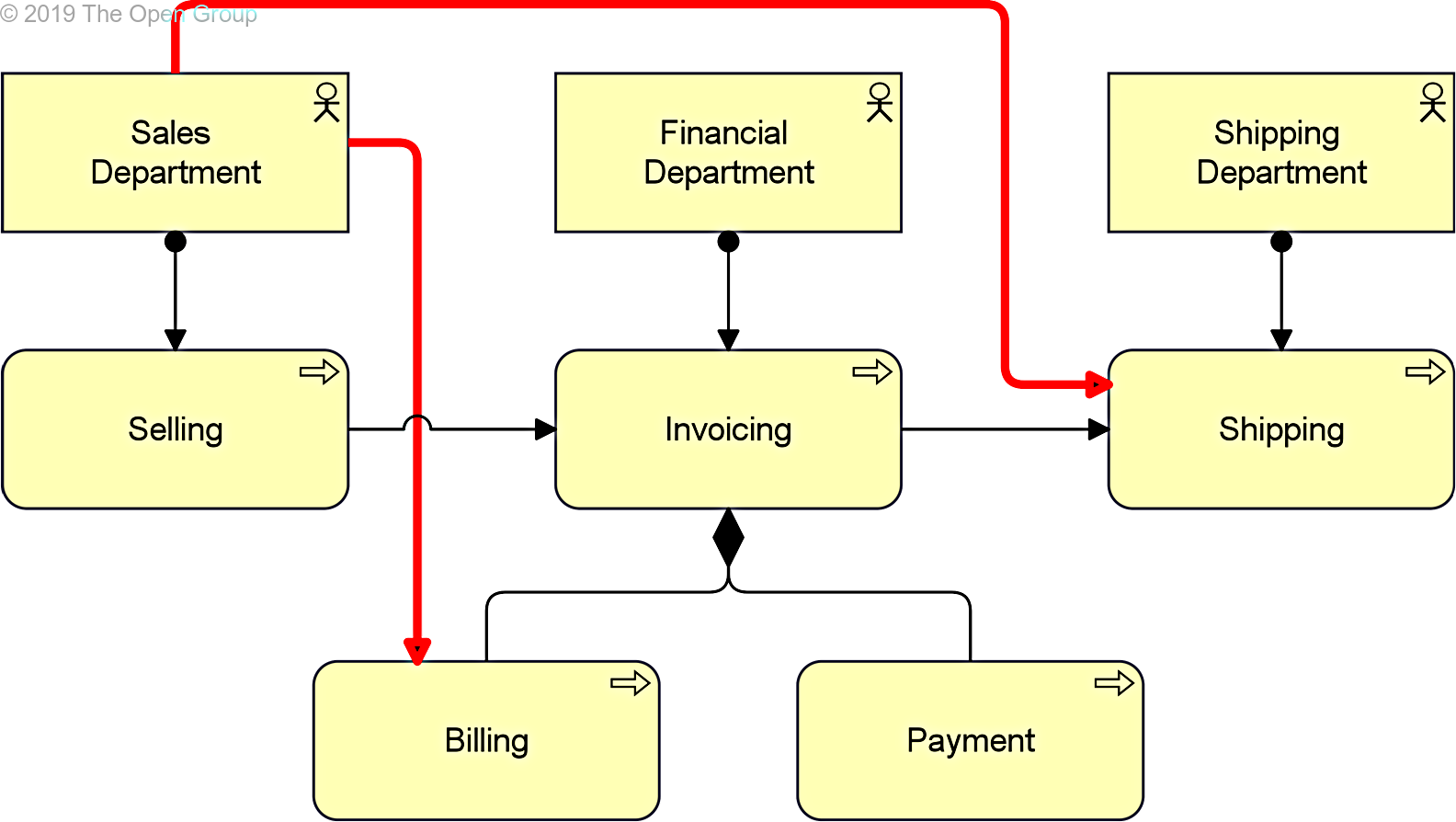
Example 47: Derivation from Triggering and Structural Relationships
B.3 Derivation Rules for Potential Relationships
The derivation rules defined so far lead to relationships that are valid with high certainty. If a model is well designed and describes a stable state of the enterprise, these derived relationships can be trusted.
This section describes derivation rules for relationships with lower certainty. They might be relevant but may also be wrong, depending on the specifics of the model. It is up to the modeler to decide on this.
The derivation rules for potential relationships are used to enrich the metamodel with relationships that otherwise would not be allowed and can be used to discover relationships in a model that otherwise might not show.
Example
Example 48 shows a potential derivation in which some relationships are valuable and some are not. In this example, an architect first modeled an application component called “Suite” that uses two infrastructure services called “Website Hosting” and “Database Hosting”. Later, the application component “Suite” was detailed by adding two composed application components “Front-end” and “Back-end”. The architect in this case did not reconsider the serving relations. Potential derivation rule PDR 5 allows the red and grey relationships. In this case, the architect determines that only the red relationships are valuable.
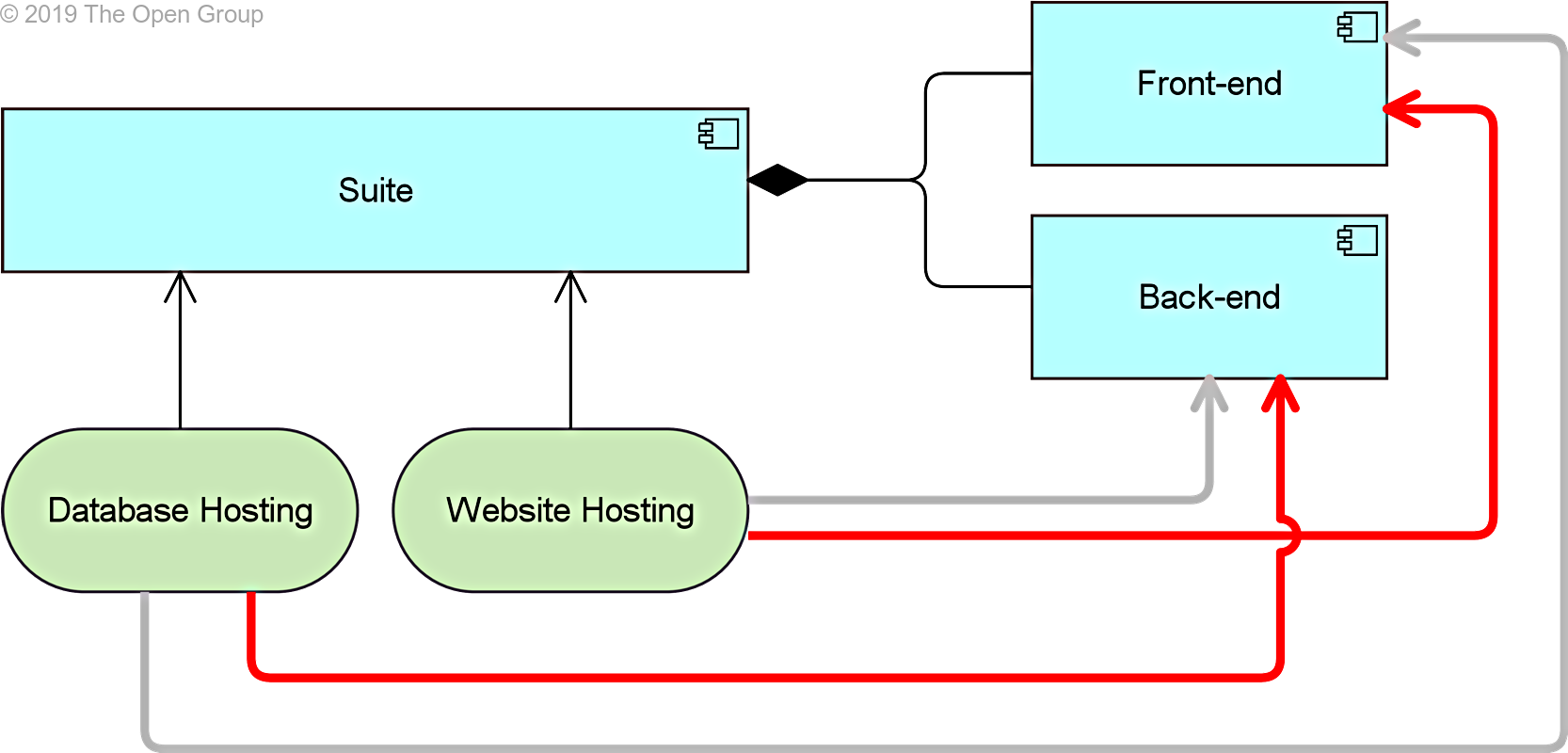
Example 48: Examples of Potential Derivation
B.3.1 Potential Derivation for Specialization Relationships
Part of the language definition is a rule that states that every relation from or to a generic element is inherited by the specialized element. This leads to a number of potential derivations.
The first two rules apply in the case where the target of a specialization relationship is the source or target of any other relationship. In this case, the source of the specialization could have the same relationship.
If two relationships p(a,b):S and q(b,c):T exist, with S being Specialization and T being a structural, dependency, or dynamic relationship, then a relationship r(a,c):T might be derived.
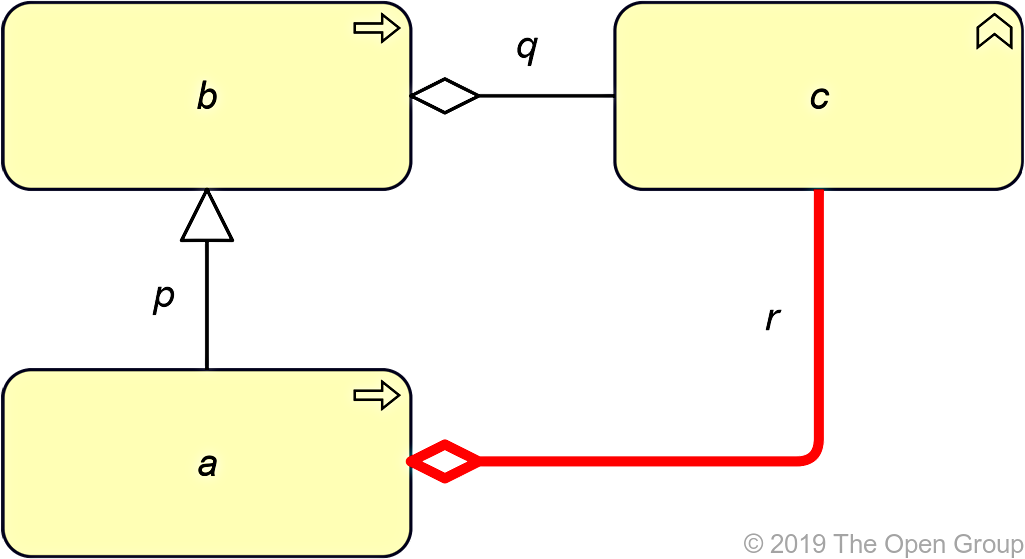
Example 49: Potential Derivation from a Specialization and Another Relationship in Line
If two relationships p(a,b):S and q(c,b):T exist, with S being Specialization and T being a structural, dependency, or dynamic relationship, then a relationship r(c,a):T might be derived.
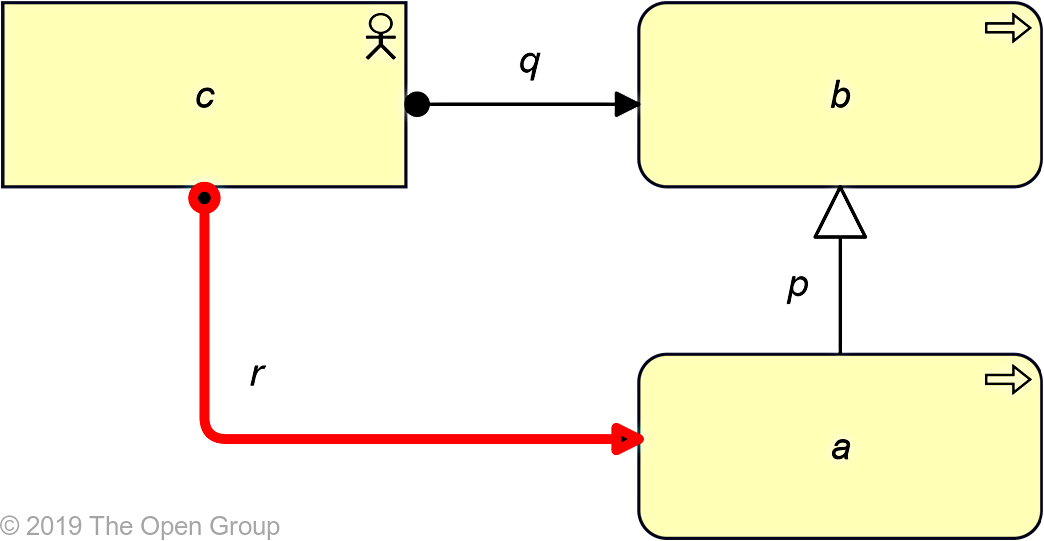
Example 50: Potential Derivation from a Specialization and Another Relationship in the Opposite Direction
The next two rules apply in the case where the target of a specialization relationship is joining the source or target of any other relationship. In this case, the source of the specialization could have the same dependency.
If two relationships p(a,b):S and q(a,c):T exist, with S being Specialization and T being a structural, dependency, or dynamic relationship, then a relation r(b,c):T might be derivable.
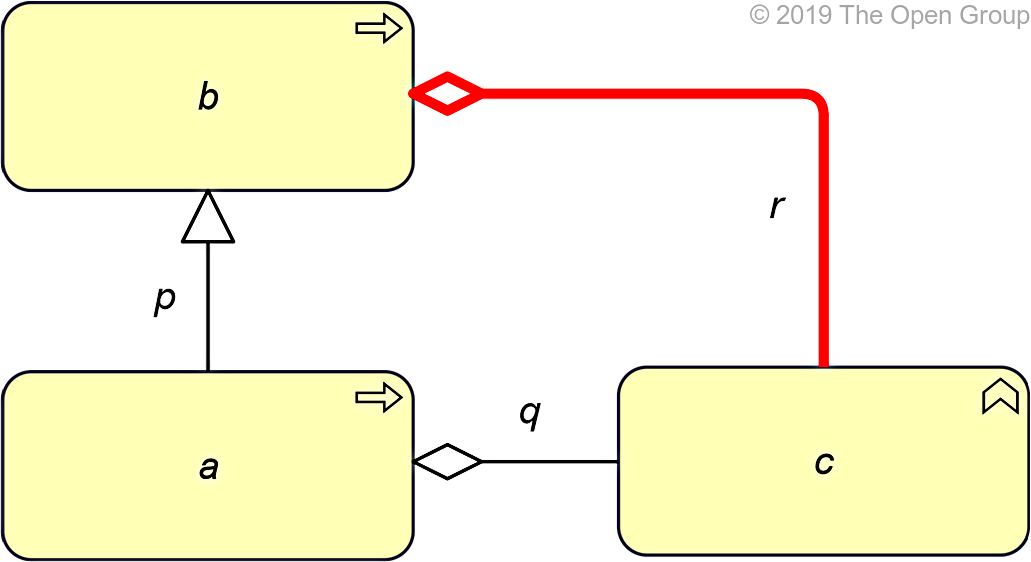
Example 51: Potential Derivation from Another Relationship and a Specialization in Line
If two relationships p(a,b):S and q(c,a):T exist, with S being Specialization and T being a structural, dependency, or dynamic relationship, then a relationship r(c,b):T might be derivable.
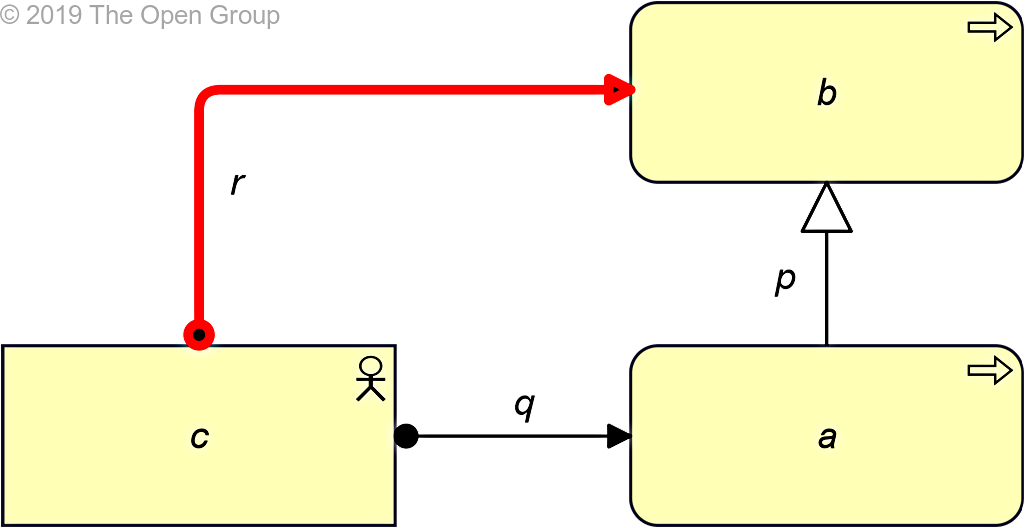
Example 52: Potential Derivation from Another Relationship and a Specialization in Line
The potential relationships derived with the rules from this section may vary a lot in likelihood, depending on the direction of the derivation (from generalized to specialized element or vice versa), the type of relationship, and the specific interpretation of the relationship. Also, a chain of multiple potential derivations usually leads to a lower probability.
Consider a model with a “Project Team” assigned to a “Project”, and an “IT Project Team”, as a specialization of “Project Team”, assigned to an I”T Project”, as a specialization of “Project”. A “Project Team” aggregates a “Project Manager”, a “Project” accesses (reads) “Project Planning”, and an “IT Project” accesses (writes) “Software Documentation” (Example 53).
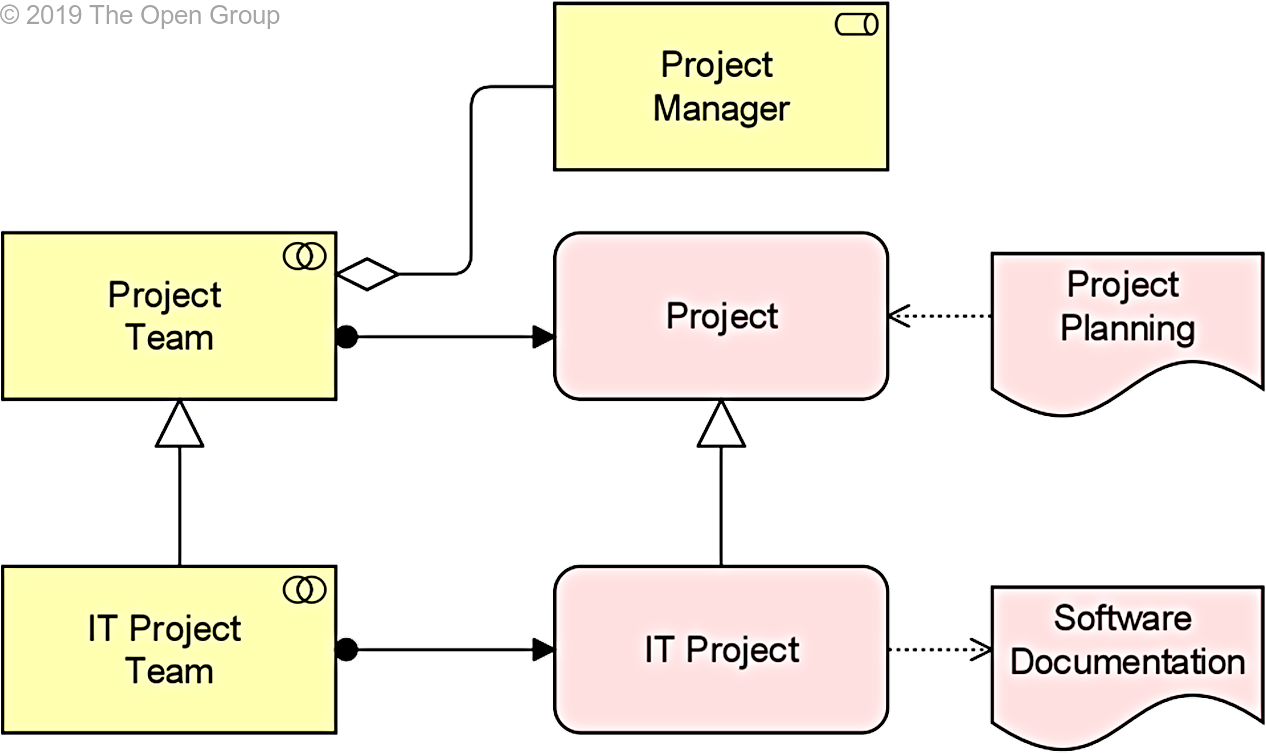
Example 53: Specializations Used in Potential Derivations
• Composition or aggregation relationships often lead to derivations that are (almost) certain when moving the source of the relationship to a specialized element (PDR 1), or the target of the relationship to a generalized element (PDR 4)
In this example, “IT Project Team” aggregates “Project Manager” is a derived relationship that is almost certain.
• For the assignments, this depends on the perspective: “IT Project Team” assigned to “Project” (PDR 1) is probably true in the sense that the “IT Project Team” always performs a “Project”, but uncertain in the sense that a “Project” is not always performed by an “IT Project Team” (e.g., if it is a business project)
For “Project Team” assigned to “IT Project” (PDR 2), this is the other way around.
• “IT Project” accesses (reads) “Project Planning” (PDR 1) is almost certainly a derived relationship, while “Project” accesses (writes) “Software Documentation” (PDR 3) is only valid for a subset of “Projects”
B.3.2 Potential Derivation for Structural and Dependency Relationships
The next two rules apply in the case where a structural and dependency relation are joining at the source of the structural relation. In this case, the target of the structural relation could have the same dependency.
If two relationships p(a,b):S and q(c,a):T exist, with S being a structural relationship and T being a dependency relationship, then a relationship r(c,b):T might be derivable.

Example 54: Potential Derivation from a Dependency and a Structural Relationship in Line
If two relationships p(a,b):S and q(a,c):T exist, with S being a structural relationship and T being a dependency relationship, then a relationship r(b,c):T might be derivable.

Example 55: Potential Derivation from a Dependency and a Structural Relationship in the Opposite Direction
B.3.3 Potential Derivation for Dependency Relationships
The next rule applies in the case where two dependency relationships are joining at an intermediate element. In this case, the two relations could be replaced by one, being the weaker of the two.
The dependency relationships are ordered by “strength”:
• Association (weakest)
• Influence
• Access
• Serving (strongest)
If two relationships p(a,b):S and q(b,c):T exist, with S and T being a Dependency Relationship, then a relationship r(a,c):U might be derivable, with U being the weakest of S and T.

Example 56: Potential Derivation from Two Dependency Relationships
B.3.4 Potential Derivation for Dynamic Relationships
The next rules apply in the case where a structural and dynamic relation are joining at an intermediate element. In this case, the target of the structural relation could have the same dependency.
If two relationships p(a,b):S and q(b,c):T exist, with S being Flow and T being a structural relationship, then a relation r(a,c):S might be derivable.
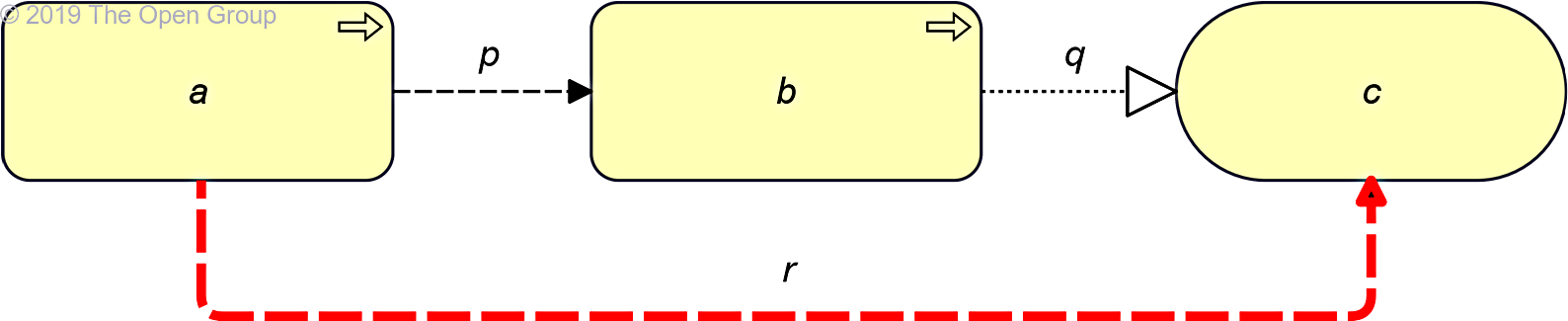
Example 57: Potential Derivation from a Dynamic and a Structural Relationship in Line
If two relationships p(a,b):S and q(a,c):T exist, with S being a structural relationship and T being a dynamic relationship, then a relationship r(b,c):T might be derivable.

Example 58: Potential Derivation from a Dynamic and a Structural Relationship in the Opposite Direction
The next rule applies in the case where two flow relationships join at an intermediate element. In this case, the flow relations could be replaced by one relation.
If two relationships p(a,b):S and q(b,c):S exist, with S being Flow, then a relationship r(a,c):S might be derivable.

Example 59: Potential Derivation from Two Flow Relationships
If two relationships p(a,b):S and q(c,b):T exist, with S being a Triggering relationship and T being a structural relationship, then a relation r(a,c):S might be derivable.

Example 60: Potential Derivation from a Triggering and Structural Relationships
B.4 Restrictions on Applying Derivation Rules
This section describes a number of restrictions that apply when using the derivation rules to infer the set of allowed relationships. In this context, the following are called “domains”:
• Motivation (Chapter 6)
• Strategy (Chapter 7)
• Core, which includes the Business Layer (Chapter 8), Application Layer (Chapter 9), Technology Layer (Chapter 10), physical elements (Chapter 11), and the location element (Section 4.5.2)
• Implementation and migration (Chapter 13)
The restrictions below apply with respect to the relationships that can be derived:
• If a is an implementation and migration element, core element, or strategy element, and b is a motivation element, only “realization” or “influence” can be derived from a to b; no relationship can be derived from b to a
• If a is an implementation and migration element or a core element, and b is a strategy element, only “realization” can be derived from a to b; no relationships can be derived from b to a
• If a is an implementation and migration element, and b is a core element, only “realization” can be derived from a to b; no relationships can be derived from b to a
• If a is in domain A and b is in domain B (which may equal A), then a relationship cannot be derived from a to b or from b to a through an intermediary c in a domain C that is distinct from both A and B
The following rules apply to access relationships and passive structure elements:
• For an element a and element b, “access” from a to b can only be derived if b is a passive structure element
• For an element a and element b, if b is a passive structure element then only “access” or “assignment” can be derived from a to b
• For an element a and element b, if a is a passive structure element then only “realization” or “influence” can be derived from a to b
And these general modeling rules must be observed:
• For two elements a and b, where b has a metamodel specialization to a (e.g., a is Node and b is Facility), all relationships that are allowed from a to a are also allowed from a to b, from b to a, and from b to b; also, given b and c, two different elements which have a metamodel specialization to a (e.g., b is Facility and c is System Software), then all relationships allowed from a to a are also allowed from b to c and from c to b
Notes:
• These restrictions only apply to derived relationships, not to relationships explicitly defined in the metamodel diagrams, which are by definition allowed
• The location element counts as a core element in these derivations
• Figure 5, Figure 12, and Figure 18, which provide the generic structure of layers, are intended as a template for these layers; the subtypes of these elements do not inherit all possible relationships with other subtypes, only with those within their own layer, as specified in the layer-specific metamodel fragments
• Product and plateau are composite elements, but can only aggregate or be composed of the specific concepts depicted in their respective metamodel fragments Figure 68 and Figure 106
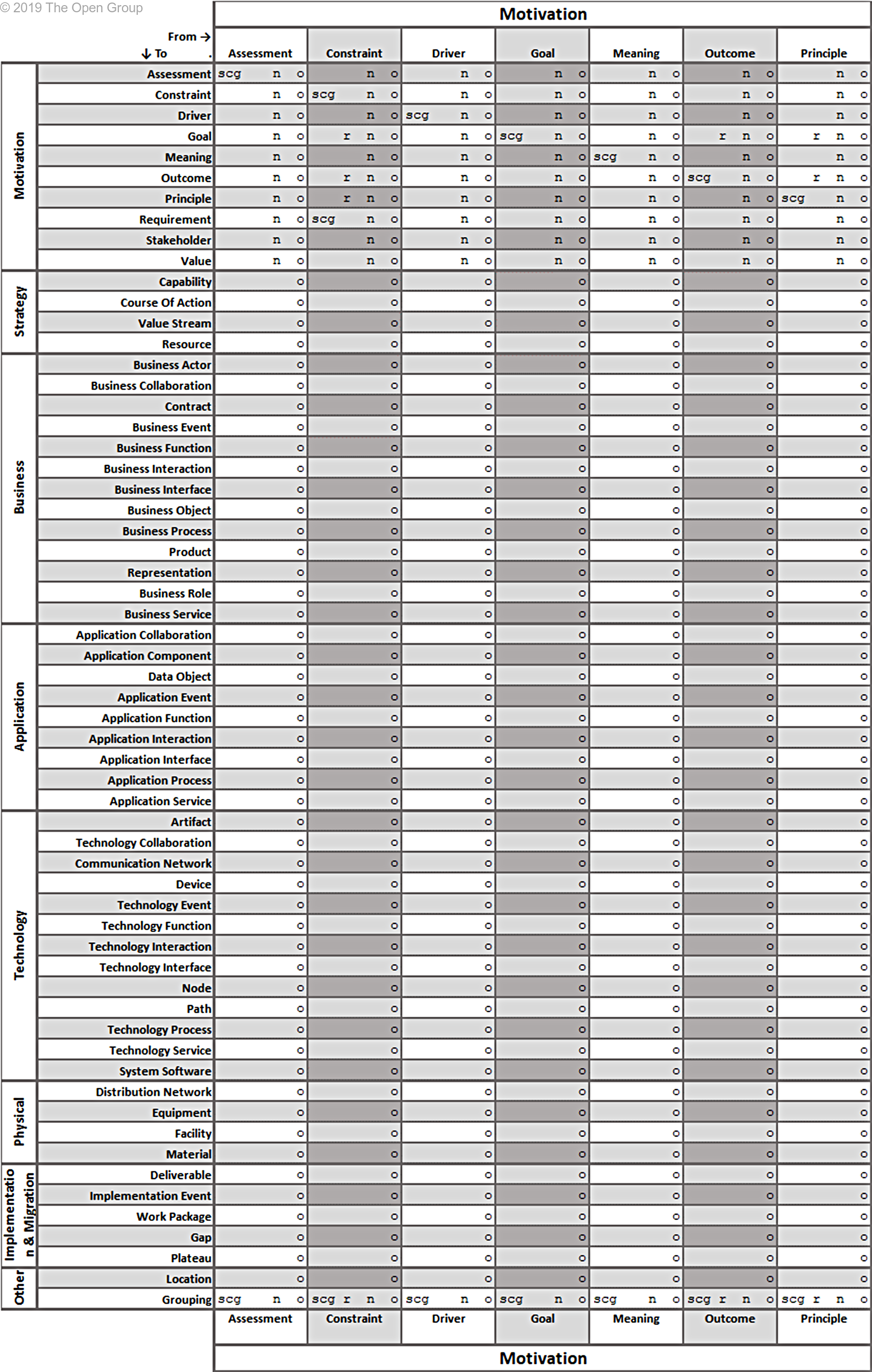
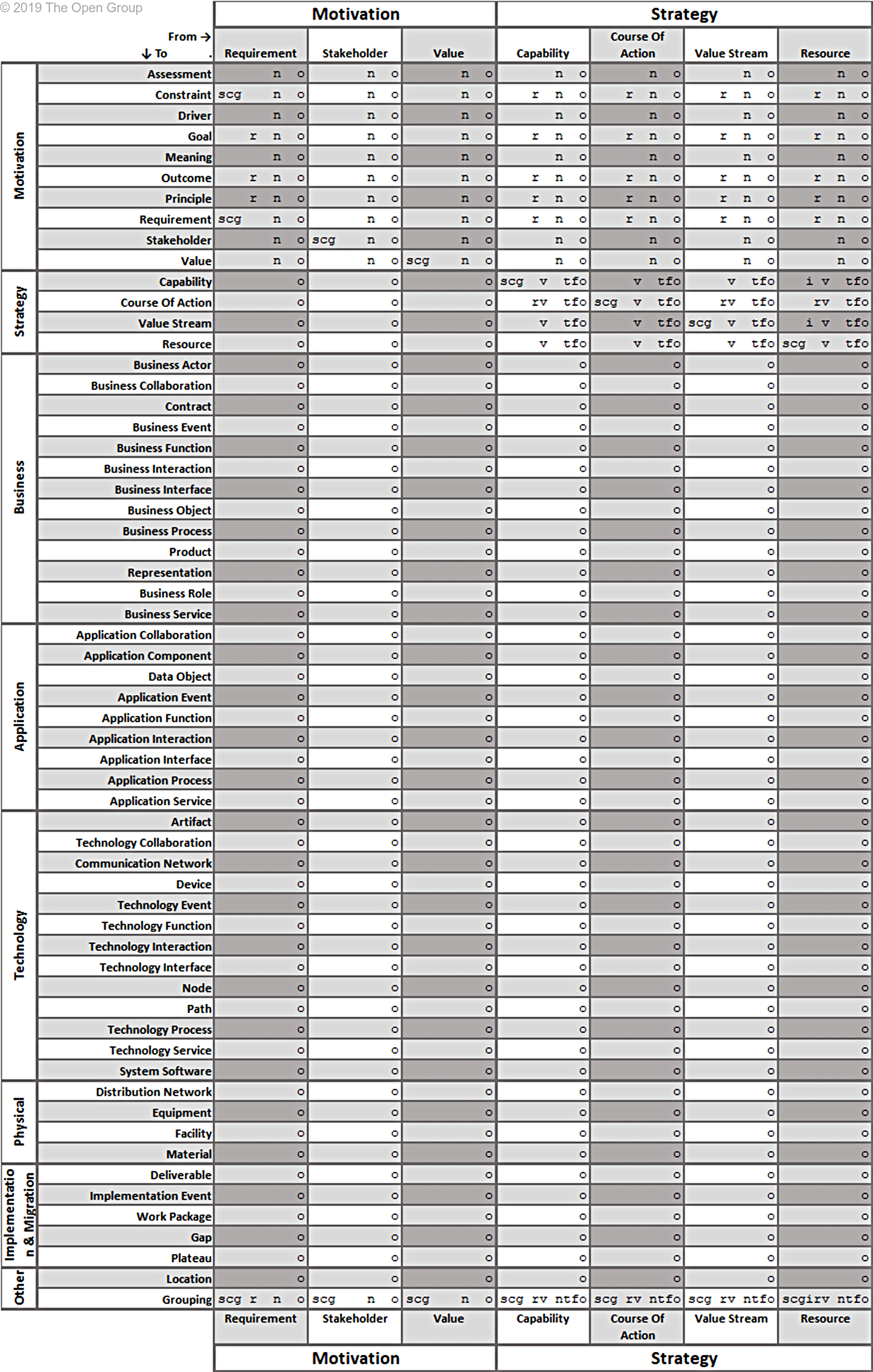
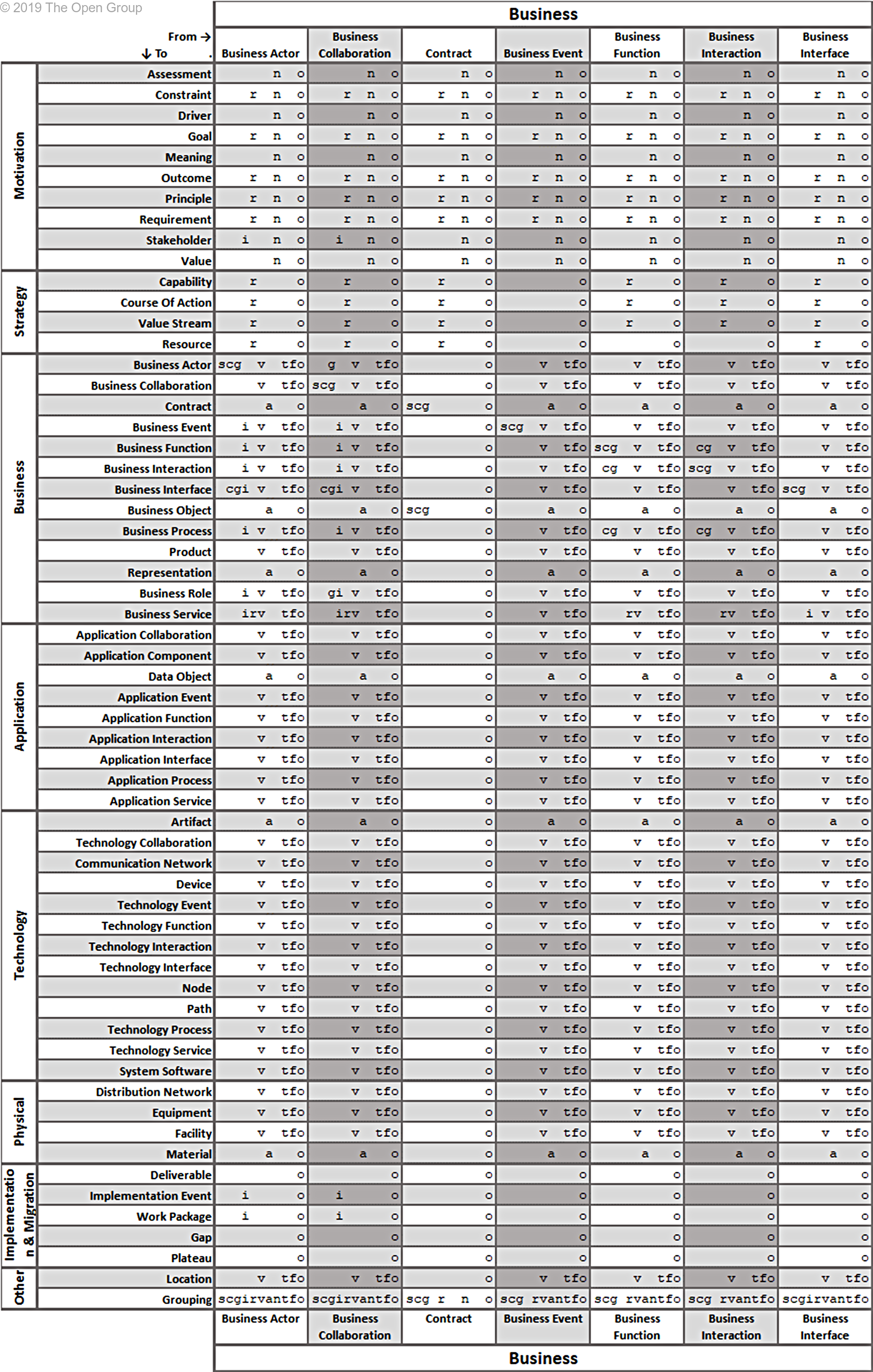
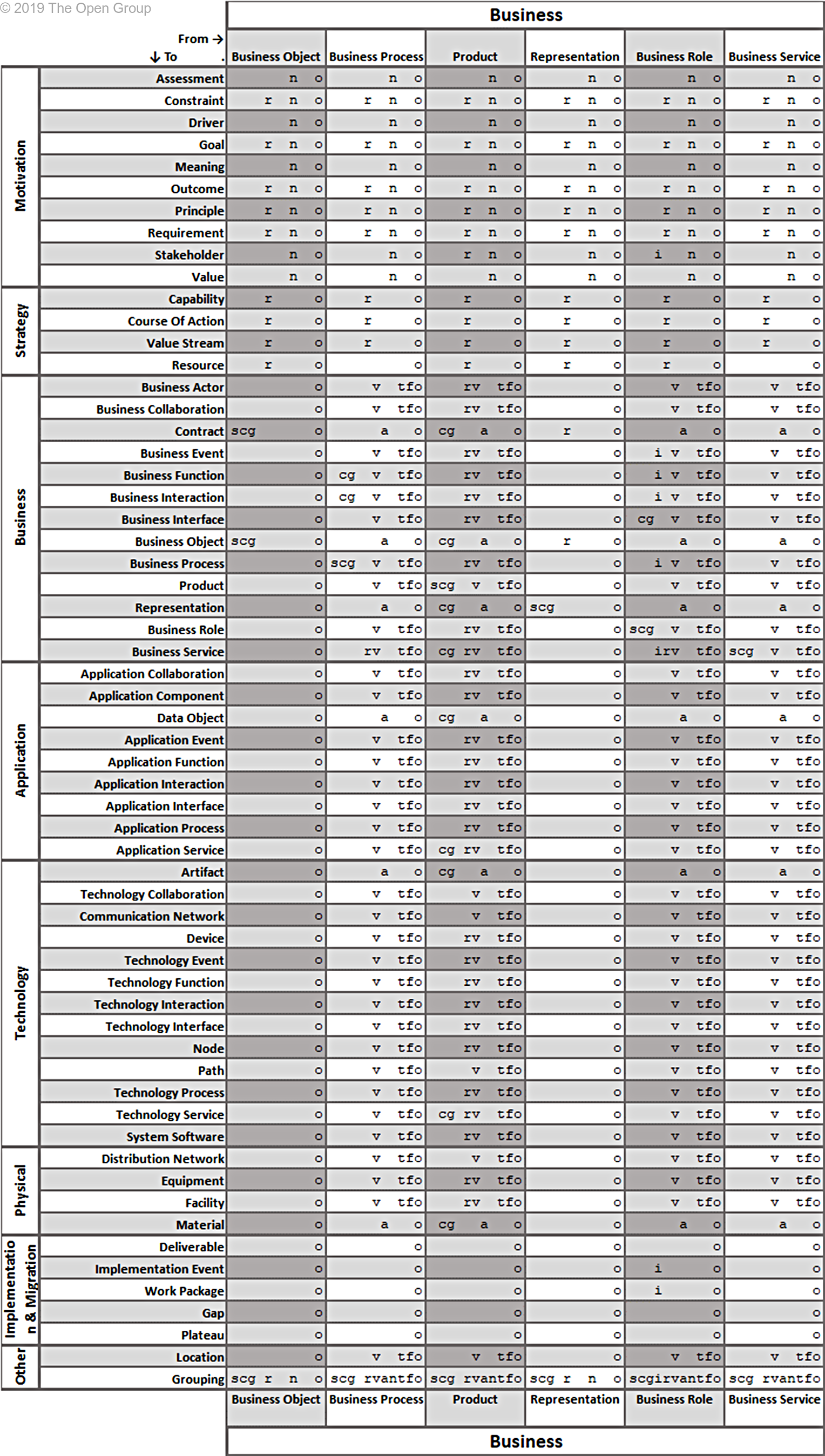
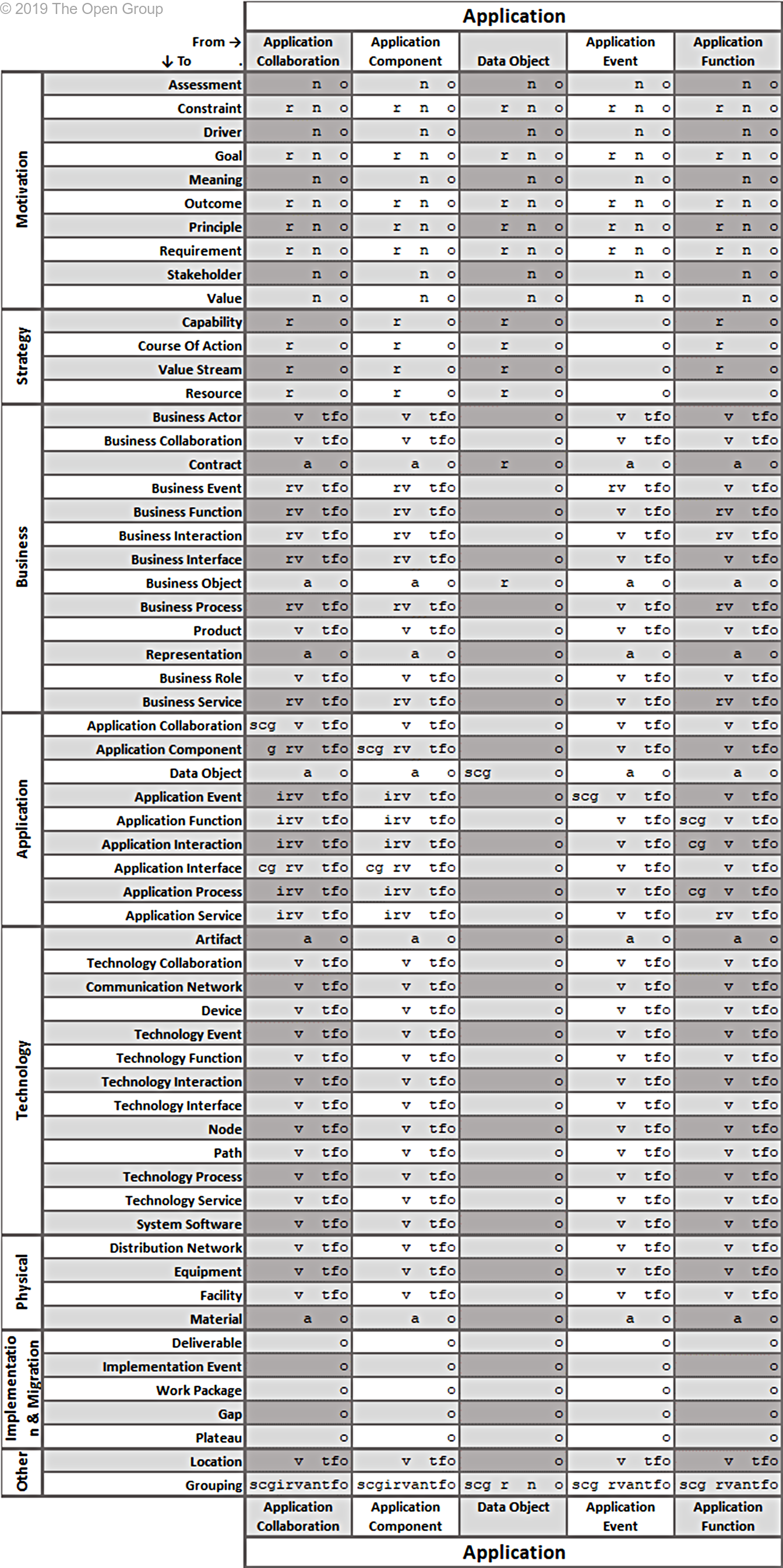
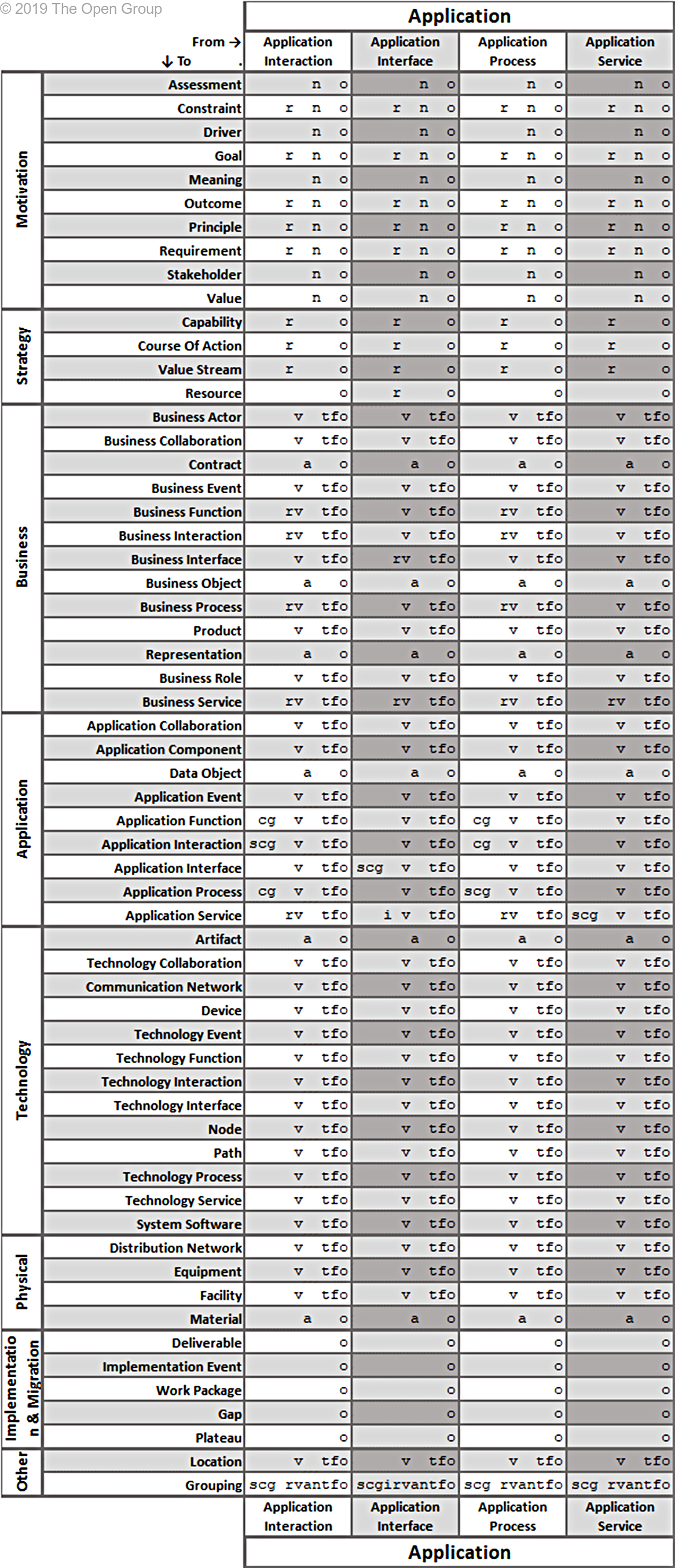
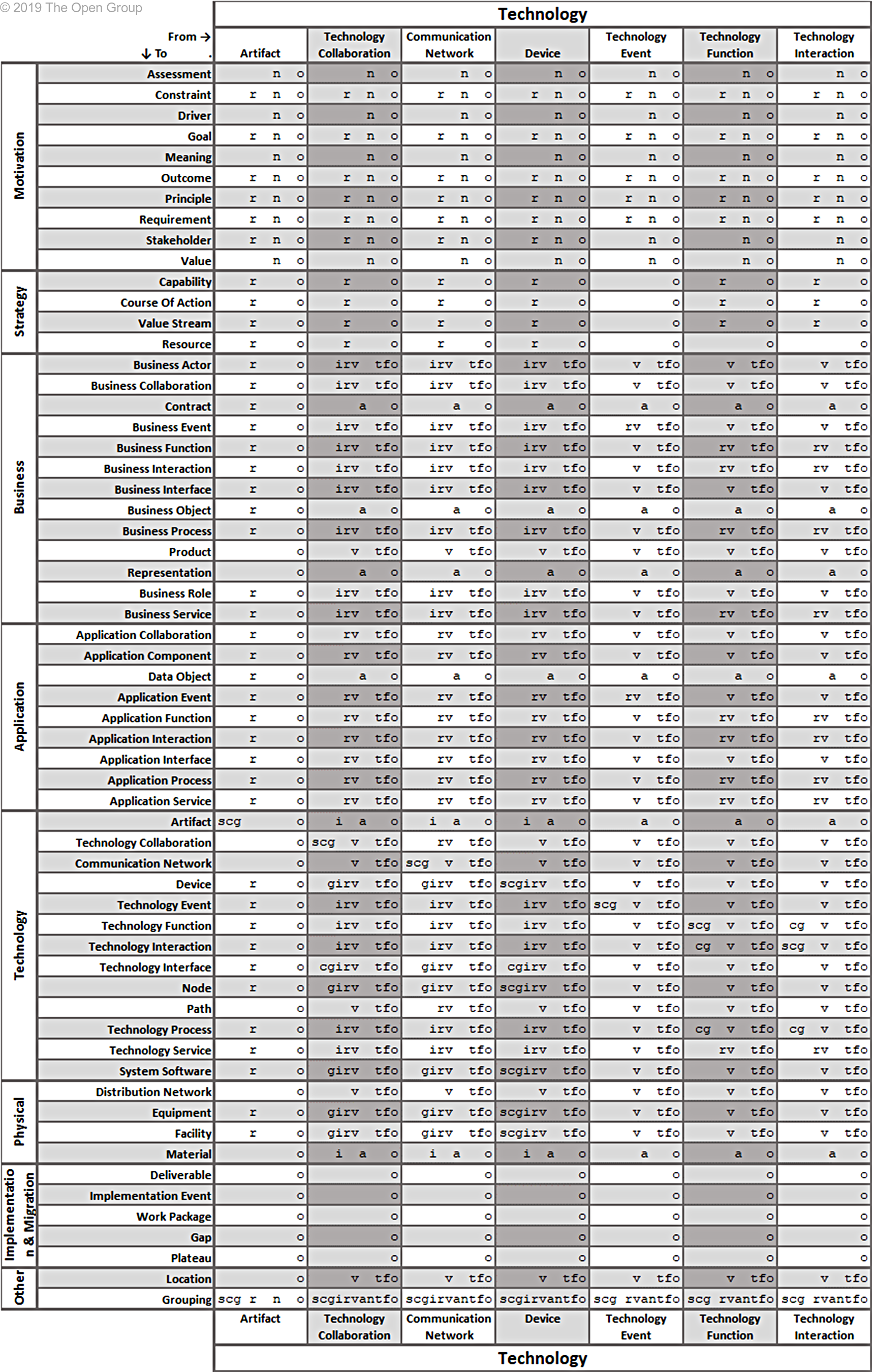
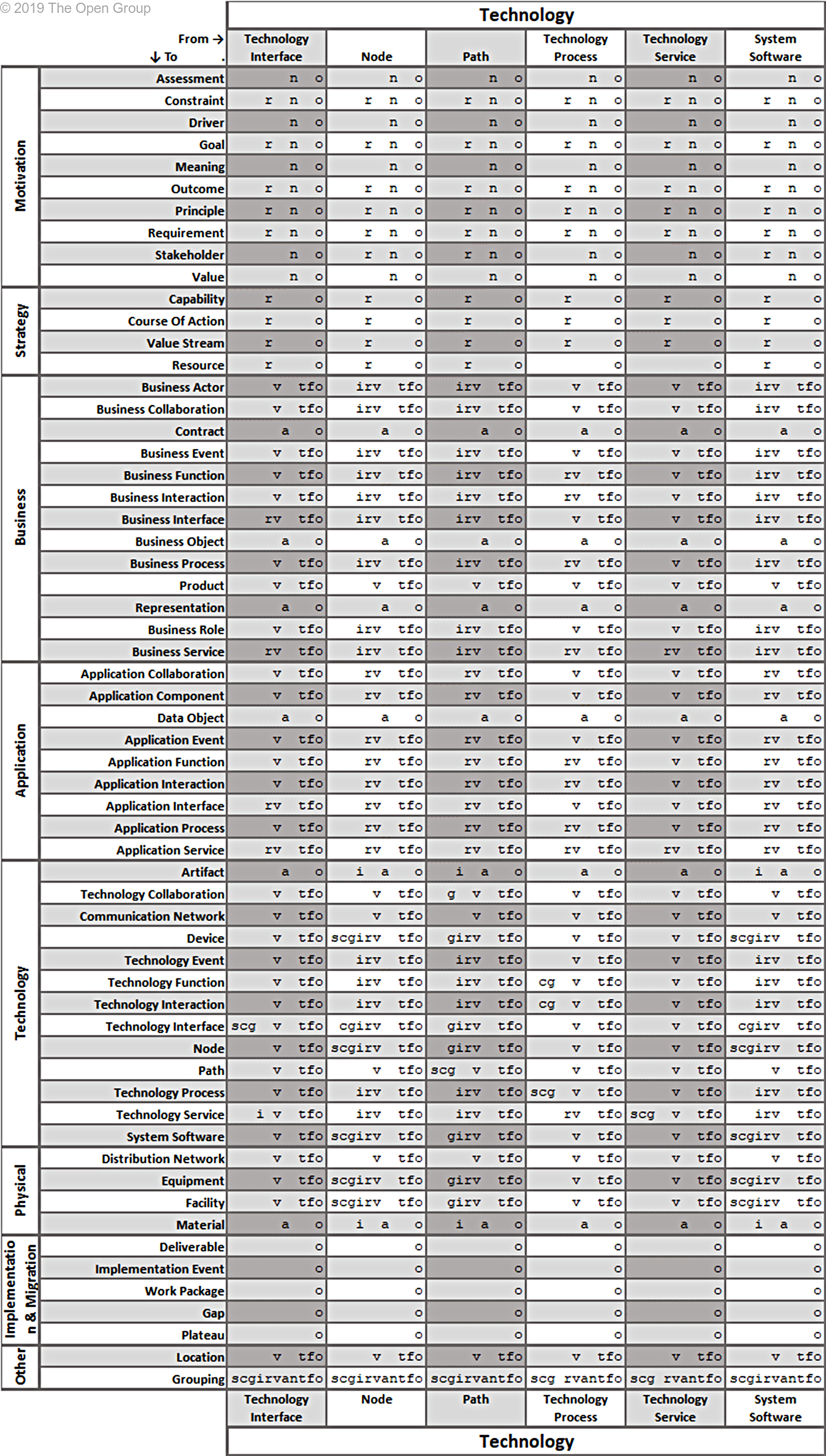
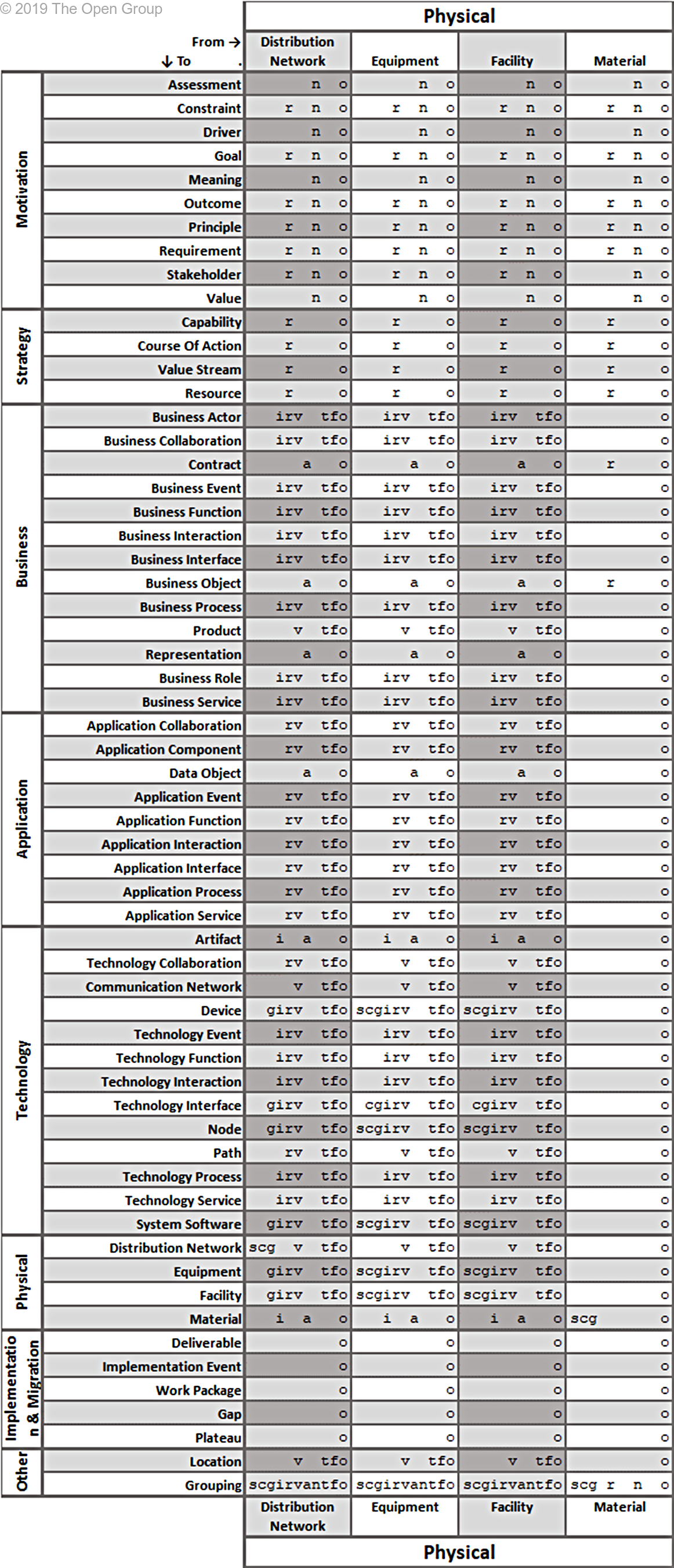
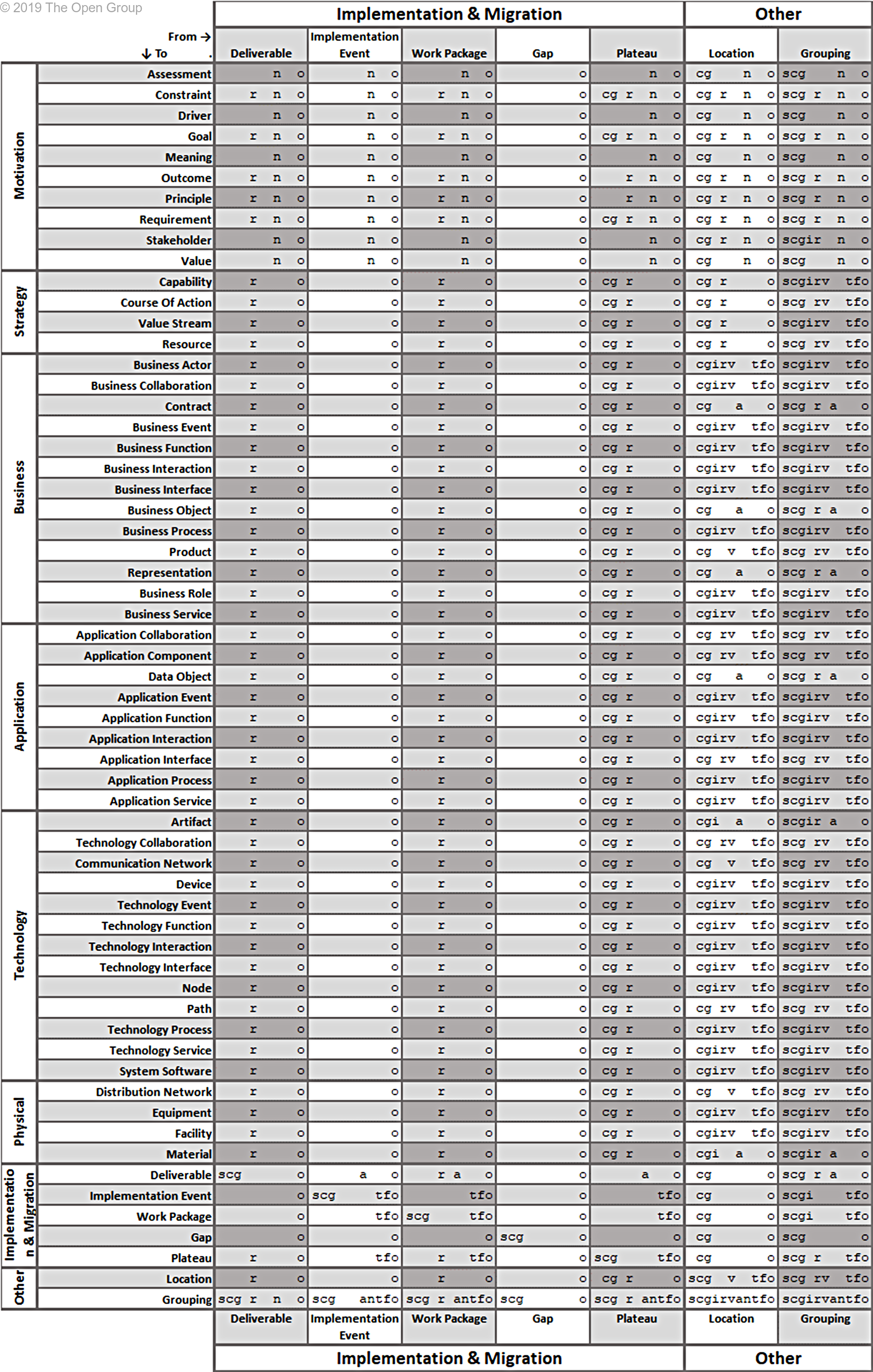
This section provides a set of tables with all allowed relationships. It is constructed from the metamodel figures in Chapters 3 through 13 and the derivation rules for relationships outlined in Section B.1.
The letters in the tables have the following meaning:
(a)ccess (c)omposition (f)low a(g)gregation ass(i)gnment
i(n)fluence ass(o)ciation (r)ealization (s)pecialization (t)riggering ser(v)ing
B.6 Grouping, Plateau, and Relationships Between Relationships
For grouping, plateau, relationships, and relationship connectors, the following conditions hold:
• Grouping and location elements may have an aggregation or composition relationship to any concept (element, relationships, or relationship connectors)
• A grouping element may be the source of any relationship with any element (provided that the element is a possible target element for the relationship)
• A grouping element may be the target of any relationship with any element (provided that the element is a possible source element for the relationship)
• A grouping element may have any relationship with another grouping element
· Any relationship may have an association relationship with any element
|
From → ↓ To |
Grouping |
Plateau/ Location |
Element other than Grouping, Plateau, Location |
Relationship |
Relationship Connector |
|
Grouping |
any |
cg + any** |
any** |
o |
afinortv* |
|
Element other than Grouping |
any* |
See metamodel. |
See metamodel. |
o |
afinortv* |
|
Relationship |
cg + o |
cg + o |
o |
|
o |
|
Relationship Connector |
afinortv |
afinortv** |
afinortv** |
o |
afinortv |
* Provided that element is a possible target element of the relationship (see Section B.5).
** Provided that element is a possible source element of the relationship (see Section B.5).
(a)ccess (c)omposition (f)low a(g)gregation ass(i)gnment
i(n)fluence ass(o)ciation (r)ealization (s)pecialization (t)riggering ser(v)ing
Downloads of the ArchiMate documentation are available under license from the Download link within the ArchiMate information web site. The license is free to any organization wishing to use ArchiMate documentation entirely for internal purposes. A book is also available from The Open Group Library as document C197.