Previous section.

DCE 1.1: Authentication and Security Services
Copyright © 1997 The Open Group

Checksum Mechanisms

Terminology, Notation, and Conventions is devoted to general terminology, notation and conventions that are used throughout this specification.

Subsequent sections of this chapter specify the (cryptographic and non-cryptographic) checksum mechanisms supported by DCE. The following list specifies all currently supported checksum mechanisms, and this chapter is therefore restricted to these checksums only:

Terminology, Notation, and Conventions

This section introduces terminology, notation and conventions, including low-level formatting details, used throughout this specification.

Use of Pseudocode

Pseudocode is employed in this and the following chapters. It has the expository purpose of explaining observable external behaviour only, and does not impose internal requirements on conforming implementations. The pseudocode notation is mostly "C-like", augmented by some other elements of standard scientific exposition (for example, "f(x) = y'' to define the value of a function f at an argument x to be y). Anything expressed in pseudocode is intended to be readily understandable by the intended audience of this specification, but if confusion can possibly result the pseudocode is also expressed in words.

Sequences

A (finite) sequence (or string or vector or n-tuple) V of length lambda(V) = n >= 0 will be denoted in order of increasing "address" (or "name" or "subscript") notation; that is, in the form V = <v0, ···, vn-1>; if n = 0, this notation degenerates to V = <>, the empty string. The n-tuple V is said to begin, at the left, with initial element v0, and to end, at the right, with final element vn-1. If 0 <= n´ < n´´ <= n-1, then vn´ is said to precede or occur before (or earlier than or to the left of) vn´´ in V, and vn´´ is said to follow or occur after (or later than or to the right of) vn´. The natural identification of a 1-tuple is always made with "the thing itself": <V> = V. Similarly, the concatenation of an m-tuple and an n-tuple are also identified with an (m+n)-tuple via <U, V> = <<u0, ···, um-1>, <v0, ···, vn-1>> = <u0, ···, um-1, v0, ···, vn-1>. In particular, <V, <>> = <<>, V> = <V> = V (via natural identifications). The terminology prepend to V refers to concatenating another vector to the beginning of V; append to V refers to concatenation to the end of V.

Bits, Bytes, Words, and so on

A bit is a boolean (binary) quantity that can take either of the values T (true) or F (false). A byte (or octet) is a sequence of 8 bits. A shortword is a sequence of 2 bytes, a word is a sequence of 4 bytes, a longword is a sequence of 8 bytes, and a quadword is a sequence of 16 bytes. By concatenation, a sequence of bits of length congruent to 0 modulo 8, 16, 32, 64 or 128, respectively, can be identified with a sequence of bytes, shortwords, words, longwords or quadwords (of the appropriate shorter length). Similarly, a sequence of bytes of length divisible by 4 can be identified with a sequence of words, and so forth.

Notes:

  1. Some other terms exist in the literature that won't be used in this specification; for example, "nibble" for a sequence of 4 bits. Also, the definitions of some of the terms above vary throughout the literature; for example, in some quarters ("16-bit architectures"), "word" means a sequence of 2 bytes, with corresponding redefinitions of "longword" and "quadword".

  2. Bits can be naturally identified with the elements of the finite field of 2 elements (integers modulo 2), F2 = {0, 1} (called the bit field in this context), via the mapping (or correspondence) defined by: F <-&#62; 0, T <-&#62; 1. And then, n-tuples of bits can be viewed as elements of the vector space Fn2 of dimension n over F2. This point of view is standard in mathematical treatments of cryptography, but it is not insisted upon here.

Integer Representations (Endianness)

The notion of "endianness" arises when one maps bit- and/or byte-sequences to (non-negative) integers. Namely, the question is whether the left (~ "big") or right (~ "little") end of the sequence is mapped to the higher value (that is, is "more significant").

First recall that any non-negative integer i has a natural 2-adic expansion (which is unique if it is the minimal 2-adic expansion; that is, if one does not allow superfluous "leading zeroes"): i = 2k-1ik-1 + ··· + 20i0 with each coefficient ij (0 <= j <= k-1, k >= 0) equal to 0 or 1 (and 2k-1 = 1). The question of endianness arises when one imposes an order on the collection of coefficients i0, ···, ik-1; that is, when one realises this collection of coefficients as a sequence. Given a mapping between coefficients and sequences, bits, bytes, shortwords, words, longwords and quadwords (or, for that matter, bit- or byte-sequences of any length) can be interpreted as non-negative ("unsigned") integers, in the ranges [0, 2k-1] where k = 1, 8, 16, 32, 64 or 128, respectively, as described below.

See Endianness for an illustration of the endianness concepts defined below. As shown there, "addresses" (names or subscripts of sequence elements) are always visualised as increasing (with respect to a fixed ordering on addresses themselves) from left to right. The meaning of big- (respectively, little-) endianness is then determined by whether sequence elements are mapped to integer power-of-2 values ("significance") in a decreasing (respectively, increasing) manner from left to right, respectively.

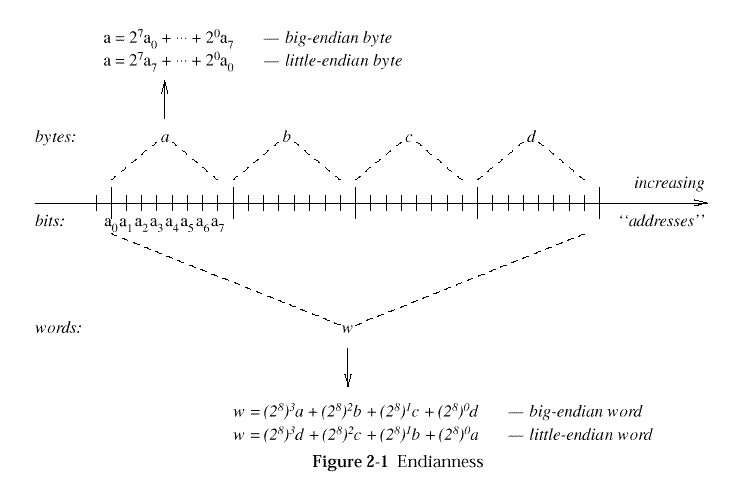Figure: Endianness
Mapping Bit-Sequences to Integers

In all mappings of bit-sequences to integers that are considered, single bits are mapped to integers via the mapping F <-&#62; 0 and T <-&#62; 1 (and these mappings are always treated as identifications, even notationally); that is, for bit-sequences of length 1 the mapping/identification are always made between bit-sequences and integers: 

 

<0> <-&#62; 0-that is, "<0> = 0"


<1> <-&#62; 1-that is, "<1> = 1"

Bytes (and more generally, any bit-sequences) can be interpreted as integers via either the big-endian (or most-significant-first) mapping, or the little-endian (or least-significant-first) mapping, which are now defined. (Other mappings of bit-sequences to integers are also possible, but not of interest.)

In big-endian mapping, the bits of the byte are considered to be ordered in decreasing significance, from the high-order or most significant bit (MSb) (on the left) to the low-order or least significant bit (LSb) (on the right). That is, for bytes (for example, bit-sequences of other lengths are similar):

<a0, a1, ···, a7> <-&#62; 27a0 + 26a1 + ··· + 20a7

And in little-endian mapping, the ordering goes the opposite way:

<a0, a1, ···, a7> <-&#62; 27a7 + 26a6 + ··· + 20a0

When one of these mappings has been chosen and fixed in a given context, it will usually be considered to be an "identification" instead of a "mapping", and the symbol "=" instead of "<-&#62;" will be used (by a common abuse of notation).

Mapping Byte-Sequences to Integers

Similarly, bytes, shortwords, words, longwords and quadwords (and more generally, any bit-sequence of length a multiple of 8 that is considered as a byte-sequence) can be interpreted, once a mapping of bytes to integers has been chosen and fixed, as integers via either big-endian or little-endian mapping (for single bytes, the two mappings coincide of course), which are now defined.

In big-endian mapping, the bytes of the byte-sequence are considered to be ordered in decreasing significance, from the high-order or most significant byte (MSB) to the low-order or least significant byte (LSB). That is, for words (for example, byte-sequences of other lengths are similar):

<a, b, c, d> <-&#62; (28)3a + (28)2b + (28)1c + (28)0d

And in little-endian mapping, the ordering goes the opposite way:

<a, b, c, d> <-&#62; (28)3d + (28)2c + (28)1b + (28)0a
Mapping Mixed Bit/Byte-Sequences to Integers

Since bit-sequences of length a multiple of 8 can also be viewed as byte-sequences, for such sequences the above mappings can be mixed to arrive at the following taxonomy of endianness for "byte/bit"-sequences.

Let W be, say, a ("word-sized") integer in the range [0, 232-1] (similar remarks hold for integers of other sizes), with 2-adic expansion:

W = 231w31 + ··· + 20w0 =
(28)3(27w31 + ··· + 20w24) + (28)2(27w23 + ··· + 20w16) +
(28)1(27w15 + ··· + 20w8) + (28)0(27w7 + ··· + 20w0)

There are then the following four bit-representations of W. Here, the terminology "X/Y-endian" (for X, Y member of {"big", "little"}) means: "X-endian with respect to bytes, the bytes being Y-endian with respect to bits". (See also Endianness .)

Of the four mappings listed above, the first two are the most important in this specification, because bytes in computer memories are invariably considered to represent integers (in the range [0, 28-1]) via the big-endian mapping. (On the other hand, bytes are variously transmitted over different serial networks in big-endian or little-endian order: the most or least significant bit may be transmitted first.) Clearly, one could extend the above ideas about endianness to include such higher-level constructs as shortword-sequences, word-sequences, and so on-the ideas are straightforward, and there is no need to elaborate on them here.

Modular Arithmetic

The usual convention is adopted that modular arithmetic on integers is denoted by "(mod n)" where n > 0 is the modulus, and the modular equivalence class of any integer N is identified with its representative in the interval [0, n-1]. That is, for any integer N (positive, negative or zero): 

 

0 <= N(mod n) <= n-1

Bitwise Operations and Rotations

The following notations for four bitwise operations will be used, all operating on bit-sequences (usually words) U, V, W of the same length:

Also, the following notation for two kinds of rotations will be used (the first is used in this chapter, the second is used in Encryption/Decryption Mechanisms ):

Notes:

  1. Note that the two kinds of rotations agree for, say, words (k = n = 32) if and only if words are identified with integers via the big/big-endian mapping-but we're using the little/big-endian mapping in the remainder of this chapter.

  2. The notations "<<<" and "<<<<" for the two left circular shift operators defined above have been adopted in analogy with the C-language "<<" operator. (The C "<<" operator is a left non-circular numerical shift operator, despite the fact that it is usually spoken of as a "bitwise" operator.)

(IDL/NDR) Pickles

By a pickle is meant an encoded/marshalled (or "linearised" or "flattened") bit-vector representation of a (value of a) data type specified in some computer language, suitable for application-level storage purposes in the absence of a communications context (hence the use of the word "pickle", meaning "preserved substance"). Pickles appear in several places in this specification.

In the case of the present revision of DCE, the only language currently supported for pickles is IDL, and the only encoding/marshalling currently supported for IDL pickles is NDR (for the specifications of the IDL language and its NDR marshalling/encoding, see the referenced Open Group DCE 1.1 RPC Specification). Therefore, for the purposes of this revision of DCE, "pickle" always means IDL/NDR pickle (specified in detail below). In essence, then, a pickle for the purposes of this specification is an in-memory representation of RPC input/output data that "normally" exists only "on-the-wire" (and hence is normally only interpreted by the RPC runtime), in a form that can be interpreted at application level.

Pickles as specified in this specification are bit-vectors (actually, byte-vectors-see below) having a common structure, which will be denoted: 

 

PKL = <H, B>

where:

Each of H and B is actually a byte-sequence (that is, has bit-length a non-negative integral multiple of 8); they will henceforth always be regarded as byte-sequences, not bit-sequences. In particular, the length of such a (byte-)vector M henceforth in this section will always mean its length in bytes.

PKL's header H is specified as an IDL data type (but whose encoding is not NDR) as follows (for the IDL definition of the data types not defined here, see Appendix N, IDL Data Type Declarations, of the referenced Open Group DCE 1.1 RPC Specification): 

 

typedef struct {
    uuid_t                              stx_id;

    unsigned32                          stx_version;
}                                           rpc_syntax_id_t;


typedef struct {
    unsigned8                           pkl_version;
    unsigned8                           pkl_length_hi;
    unsigned16                          pkl_length_low;
    rpc_syntax_id_t                     pkl_syntax;

    uuid_t                              pkl_type;
}                                           idl_pkl_header_t;

The fields of these data types are the following:

Here, "encoding a UUID in big/big-endian format" means that the UUID's string representation (see Appendix A, Universal Unique Identifier, of the referenced Open Group DCE 1.1 RPC Specification) is to have its hyphens removed, and the resulting 32-character string interpreted as a hexadecimal integer, which is then encoded in big/big-endian format. Thus, for example, the UUID (in string representation) 01234567-89ab-cdef-0123-456789abcdef is mapped to the byte vector <0x01, 0x23, 0x45, 0x67, 0x89, 0xab, 0xcd, 0xef, 0x01, 0x23, 0x45, 0x67, 0x89, 0xab, 0xcd, 0xef> (where "0x" is the usual C-language hexadecimal prefix notation, and where each byte is bit-encoded in big-endian format). (This definition can also be formulated equivalently in terms of big/big-endian encodings of the individual fields of a uuid_t-see Appendix N, IDL Data Type Declarations, of the referenced Open Group DCE 1.1 RPC Specification- but this is not done here.)

Note that the encoding/marshalling of the fields of rpc_syntax_id_t and of idl_pkl_header_t is included in their specifications above (namely, it is always big/big-endian, not NDR). It is further specified that the encoded order of the fields of rpc_syntax_id_t and of idl_pkl_header_t is the same order as the syntactic listing of the fields in their IDL structure definitions, above; and there are no "padding" bits. Thus, according to this encoding specification, the encoded/marshalled length of idl_pkl_header_t is 40 bytes, formatted as follows (using C-like "dot notation" for structure fields, and using subscripts for sizes in bytes): 

 

<pkl_version1,
<pkl_length_hi1, pkl_length_low2>,
<pkl_syntax.stx_id16, pkl_syntax.stx_version4>,
pkl_type16>

PKL's body bgcolor="#FFFFFF" B depends on PKL's syntax (that is, PKL's syntax field, H.pkl_syntax). The pickle bodies for the currently supported pickle syntaxes are specified as follows:

Note:
Fully-fledged support for pickling (or "encoding services"), as opposed to the "hand-rolled" pickles described in this section, is anticipated in a future revision of DCE.

CRC-32

This section specifies the "non-cryptographic" checksum mechanisms employed in this specification. Only one such type of mechanism, CRC-32, is currently supported, so this whole section is devoted to that.

Notes:

  1. This section is based on, and (unless stated otherwise) is technically aligned with, CCITT V.42. However, for editorial reasons, this section stands independently, and no familiarity with that document is required. (Thus, the part of this chapter that duplicates information in the cited document is intended to be technically equivalent to that document, rewritten for the expository purposes of this document, and any technical discrepancies between the two are inadvertent and to be reconciled.)

  2. CRC-32 is used in this specification primarily in Key Distribution (Authentication) Services (Kerberos, see Registered Encryption Types ), and in Protected RPC 1 (Protected RPC). It also makes a minor appearance in rs_acct_key_transmit_t .

Cyclic Redundancy Checksums

Cyclic redundancy checksums (CRCs) are defined abstractly in terms of polynomials with modulus-2 coefficients (that is, in terms of the polynomial ring F2[X] in the indeterminate X), as follows. (Note that in this abstract definition there is no need to specify any conventions regarding identifications (endianness) of bit-sequences with integers.)

For purposes of this definition, identify arbitrary non-empty bit-vectors V of length k > 0 with polynomials V(X) regarded as having highest power k-1 via the following big-endian correspondence:

V = <v0, ···, vk-1> <&#173;-> V(X) = v0Xk-1 + ··· + vk-1X0

Here, V(X) is regarded as having "highest power" k-1, though not necessarily "degree" k-1, since some of its leading coefficients v0, v1, ···, may be 0.

Now fix an integer N > 0 (for the purposes of DCE, N will always be 32), and fix a polynomial G(X) member of F2[X] of degree exactly N (that is, the coefficient of XN in G is non-zero). Then, for any S(X) = s0XN-1 + ··· + sN-1X0 regarded as having highest power N-1, and any M(X) = m0XK-1 + ··· + mK-1X0 regarded as having highest power K-1 (K > 0), there exist unique polynomials Q(X) and R(X) (depending on K, S(X), G(X) and M(X)), such that:

This follows from the elementary technique of polynomial long division (using modular arithmetic with modulus 2 on the coefficients); that is, Q(X) is the quotient and R(X) is the remainder of the division of XKS(X) + M(X) by G(X). Note that under the (big-endian) identification of bit-vectors with polynomials, the correspondence is as follows:

XKS(X) + M(X) = s0XK+N-1 + ··· + sN-1XK + m0XK-1 ··· + mK-1X0 <&#173;->
<s0, ···, sN-1, m0, ···, mK-1>

(That is, in terms of bit-vectors, the polynomial XKS(X) + M(X) corresponds to prepending (the bits of) S(X) to (the bits of) M(X).)

Now by definition, the N-bit CRC of an arbitrary non-empty "bit-message" M, with respect to the generator G and the seed (or initialisation vector) S (identifying bit-vectors and polynomials as above, of course), is the N-bit vector <r0, ···, rN-1> identified with the remainder polynomial R(X) as described above. The notation for this CRC is: 

 

CRCG(S, M)

In the common case of the seed S being 0 (that is, a 0-vector or 0-polynomial), the notation CRCG(0, M) is sometimes simplified to: 

 

CRCG(M)

With this notation, the following CRC composition law (or chaining property) is immediately seen to hold:

CRCG(S, <M, M´>) = CRCG(CRCG(S, M), M´)

Now suppose further that the generator G(X) is irreducible (that is, G(X) cannot be expressed as a product of two polynomials of positive degree). Then N-bit CRCs based on G(X) have the error-detecting property that any two distinct messages differing in at most a subsequence of N bits have distinct CRCs (it also detects "most" other errors, in a sense not described here). That property, while important for the data communications heritage of CRCs, is not significant for this chapter. Instead, for the purposes of this specification, the significant property met for CRCs based on irreducible generators is the "probabilistic collision-resistance" property mentioned previously. (Note that any given message can easily be modified-by appending a single 32-bit word to it-to yield any given CRCG-checksum value, so that CRCs are not "cryptographically collision-resistant".)

Finally, a "twisted" version of CRCs is defined as follows. Let "§" denote the bit-reflection (or bit-reversal) operation, which is defined on arbitrary bit-vectors V = <v0, ···, vk-1> by:

V§ =
<v0, ···, vk-1>§ =
<vk-1, ···, v0>

Likewise, let "§&#167;" denote the per-byte bit-reflection operation, which is defined on bit-vectors M as follows. First, if M is not a byte-vector; that is, if the bit-length of M is not a positive multiple of 8, append the minimal number of zero-bits to it such that the resulting bit-vector (still denoted M, by abuse of notation) does have bit-length a positive multiple of 8. Then, define the per-byte bit-reflection of the resulting byte-vector M by:

M§&#167; =
<<m0···, m7>, ···, <m8l+0, ···, m8l+7>>§&#167; =
<<m0, ···, m7>§, ···, <m8l+0, ···, m8l+7>§> =
<<m7, ···, m0>, ···, <m8l+7, ···, m8l+0>>

Then with these notations, the twisted CRC corresponding to CRCG, denoted CRC§G, is defined for bit-vectors M as follows:

CRC§G(S, M) = (CRCG(S§, M§&#167;))§

If the seed S is 0, the notation CRC§G(0, M) is sometimes simplified to: 

 

CRC§G(M)

Note that twisted CRCs still satisfy the CRC chaining property (for byte-vectors M, M´):

CRC§G(S, <M, M´>) = CRC§G(CRC§G(S, M), M´)
Note:
The twisting convention is related to the data communications heritage of CRCs: bytes in computer memories are often communicated across serial data lines least-significant-bit-first. That is, while "in-core" bytes are invariably interpreted as big-endian, they are often (but not always) twisted to become little-endian bytes "on-the-wire".

The specific irreducible generating polynomials, G(X), currently registered in DCE are collected in Registered CRCs .

Registered CRCs

The only CRC currently used in DCE arises by taking G(X) to be the following specific choice of irreducible generating polynomial (of degree N = 32), said to be the CCITT-32 (or ITU-T, OSI/IEC, Autodin-II, Ethernet, FDDI, PKZip, and so on) polynomial:

GCCITT-32(X) =

X32 + X26 + X23 + X22 + X16 + X12 + X11 + X10 + X8 + X7 + X5 + X4 + X2 + X1 + X0

If the X32-term is ignored (or rather, considered to be implicitly present, since the X32-term of a 32-degree generating polynomial must always be present), this polynomial corresponds, according to the (big-endian) identification of polynomials with bit-vectors, to the bit-vector: 

 

GCCITT-32(X) =


<0,0,0,0, 0,1,0,0, 1,1,0,0, 0,0,0,1, 0,0,0,1, 1,1,0,1, 1,0,1,1, 0,1,1,1>
Note:
This bit-vector in turn corresponds to various integers under the various identifications of bit-vectors with integers. For example, under the big/big-endian identification it corresponds to the integer 0x04c11db7 = 79764919, and under the little/little-endian identification it corresponds to 0xedb88320 = 3988292384. These integer representations are of no interest for the purposes of this specification, though they may be of some use for particular implementations.

This CCITT-32 CRC, being the only CRC used in DCE, will henceforth be denoted simply, without fear of confusion: ("the") CRC-32 (this is perhaps a slight abuse of terminology, though a commonly accepted one, because "CRC-32" is sometimes also used as a generic term meaning "an N-bit CRC where N = 32"). Accordingly, this CCITT-32 CRC and its twisted version (which is the version actually used in Protected RPC ) will henceforth be denoted simply: 

 

CRC32(S, M)


CRC§32(S, M)

If S = 0, the notation is sometimes simplified to: 

 

CRC32(M)


CRC§32(M)

MD4

This section specifies MD4, one of the "cryptographic" checksum mechanisms employed in this specification.

Note:
This section is based on, and (unless stated otherwise) is technically aligned with, the Internet document RFC 1320, by R. Rivest, dated April 1992. However, for editorial reasons, this section stands independently, and no familiarity with that document is required. (Thus, the part of this section that duplicates information in the cited document is intended to be technically equivalent to that document, rewritten for the expository purposes of this document, and any technical discrepancies between the two are inadvertent and to be reconciled.)

MD4 is described by an algorithm that takes as input a bit-message M of arbitrary length and produces as output a 128-bit message digest (or hash, checksum, checksumtext, fingerprint) of M. MD4 is a non-invertible ("one-way") function, and it is claimed that it has the cryptographic property of being collision-resistant (or collision-"proof"): it is computationally infeasible to exhibit (that is, to produce, generate or construct) two distinct messages having the same message digest as one another, or to exhibit a single message having a given prespecified message digest. More precisely, it is claimed that the "difficulty" (computational complexity) of exhibiting two distinct messages having the same message digest has average order O(½·264), and that the difficulty of exhibiting a single message having a given message digest has average order O(½·2128).

Let M = <m0, ···, mn-1> be an arbitrarily given bit-message (sequence) of length n bits. Here n is an arbitrary non-negative integer (it may be 0, it need not be congruent to 0 (mod 8), and it may be arbitrarily large). Then the algorithm below is performed to compute the message digest of the message M, which is denoted by MD4(M).

For the remainder of this section, the little/big-endian identification of integers and 32-bit vectors is used (as defined in Mapping Mixed Bit/Byte-Sequences to Integers ).

Some Special Functions

The following four special functions are defined for use in the MD4 algorithm. Let U, V, W be 32-bit vectors (or, what amounts to the same given the fixing of the little/big endian correspondence in the remainder of this section, integers in the range [0, 232-1]).

Note:
It is interesting (from a cryptographic design perspective) to note that various observations can be made about these functions (even though these observations are quite unnecessary from a DCE conformance point of view). For example, it may be noted that F acts as the conditional: "if U then V else W" (or in C-language notation, "U?V:W"). The function F could have been defined using "addition (mod 232)" instead of "|", since "U & V" and "(~U) & W" will never have 1s in the same bit position. In each bit position, G acts as the majority function: if at least two of (the bits of) U, V, and W are set, then the corresponding bit of G(U, V, W) is set, otherwise it is reset. If the bits of U, V and W are independent and unbiased in the statistical sense, then each bit of F(U, V, W) will be independent and unbiased. The functions G and H are similar to the function F, in that they act in "bitwise parallel" to produce their output from the bits of U, V and W, in such a manner that if the corresponding bits of U, V and W are independent and unbiased, then each bit of G(U, V, W) and H(U, V, W) will be independent and unbiased. The function H is just the parity function of its inputs (that is, each bit position of its output is the bit sum (mod 2) of its inputs).

Append Padding Bits

The message M is padded (appended to), to produce a new bit-message of bit-length n´ = lambda(M´) > n and n´ equivalence 448 (mod 512) (the meaning of the "magic number" 448 is merely that 448 + 64 = 512-see Append Length on the significance of the number 64): 

 

M' = <M, 1, <0, ···, 0>>;

Padding is always performed, even if the length of the original message M is already congruent to 448 (mod 512). It is performed as follows: a single "1" bit is appended to the message (on the right), and then a 0-vector (one consisting entirely of (zero or more) "0" bits) is appended, so that the length in bits of the padded message becomes congruent to 448 (mod 512). In all, at least 1 bit and at most 512 bits are appended.

Append Length

The padded message M´ is appended with the 64-bit representation of n (mod 264), to produce the new bit-message of bit-length n´´ = lambda(M´´) = n´ + 64: 

 

M" = <M', n(mod 264)>;

Namely, write n (mod 264) as an integer, as described above, and then append the 8 bytes of this longword (in little/big-endian order) to the end of the padded message M´ from the previous step.

The result is now n´´ equivalence 0 (mod 512). As described above, M´´ can also be viewed as a sequence of words: let M´´[0], ···, M´´[N-1] denote these words, where N = n´´/32 equivalence 0 (mod 16).

Note:
This step has the theoretical limitation that it does not distinguish between messages that differ in length by multiples of 264. In practice this is not a significant limitation (in particular, it does not pose a significant security threat), for two reasons:

  1. "For all practical purposes", it may be assumed that all messages have length less than 264. This is because the length of time it would take to merely transmit (over RPC or any other medium) a message of length 264 bits (much less compute its MD4 checksum) is impractically large. Indeed, at a transmission rate of one gigabit (109 bits) per second, it would take ~584½ years just to transmit such a message. Adding to this transmission time any actual local processing time on the data (such as "generating" it on the sending side, or "interpreting" it on the receiving side) reduces to insignificance the practical uses of such very large messages (in the present era of computing).

  2. In the actual usage of MD4 as specified in DCE (namely, in Protected RPC), all messages actually protected with MD4 have length < 264 (see Protected RPC , and the referenced Open Group DCE 1.1 RPC Specification).

Initialise State Buffer and Trigonometric Vector

A quadword (= 128 bits) (external) state buffer, denoted <A´, B´, C´, D´>, is used to describe the pseudocode computation below. Here, each of A´, B´, C´, D´ is a word-sized variable. These variables are initialised to the following initialisation values or seeds (expressed as integers in C-like hexadecimal notation, with the corresponding little/big-endian byte-sequences in comments): 

 

A' = 0x67452301; /* = <0x01,0x23,0x45,0x67> */
B' = 0xefcdab89; /* = <0x89,0xab,0xcd,0xef> */
C' = 0x98badcfe; /* = <0xfe,0xdc,0xba,0x98> */
D' = 0x10325476; /* = <0x76,0x54,0x32,0x10> */

The following array of 2 "quadratic" (unsigned) words, Q[2] and Q[3] is further initialised: 

 

Q[2] = 0x5a827999;
Q[3] = 0x6ed9eba1;
Note:
The origin of the name "quadratic" comes from the fact that Q[i] = [232·sqrt(i)], where on the right hand side "[···]" denotes the integral part of a real number, and "sqrt" is the usual square root function. The values Q[2] and Q[3] are chosen for use in the MD4 algorithm because the bits of these 2 values are statistically well-distributed for this application.

Compress Message in 16-Word Chunks

Perform the following algorithm (expressed in pseudocode).

Its outer loop processes the padded, appended message M´´ in chunks of 16 words (= 512 bits) as follows: 

 

for (i = 0; i <= N/16 - 1; i += 1) {
        <A',B',C',D'> =
            COMPRESS(A',B',C',D',M"[16*i+0],···,M"[16*i+15]);
}

Its inner compression function, denoted COMPRESS(A´, B´, C´, D´, R[0], ···, R[15]), takes as input a 128-bit state vector <A´, B´, C´, D´> and a 512-bit message chunk <R[0], ···, R[15]>, and produces as output a 128-bit state vector, say <A´´, B´´, C´´, D´´>. It is defined by the following algorithm (consisting of 3 rounds of 16 compression operations each), where "+" denotes ("unsigned") addition (mod 232), and where F, G and H are the special functions defined in Some Special Functions : 

 


/* Initialise internal state buffer <A,B,C,D> = <A',B',C',D'>. */
A = A'; B = B'; C = C'; D = D';

/* Round 1 -- Let "FF{abcd,r,s}" denote the F-compression statement
           a = (a + F(b,c,d) + R[r] <<< s
   and invoke it 16 times as follows: */
FF{ABCD, 0, 3}; FF{DABC, 1, 7}; FF{CDAB, 2,11}; FF{BCDA, 3,19};
FF{ABCD, 4, 3}; FF{DABC, 5, 7}; FF{CDAB, 6,11}; FF{BCDA, 7,19};
FF{ABCD, 8, 3}; FF{DABC, 9, 7}; FF{CDAB,10,11}; FF{BCDA,11,19};
FF{ABCD,12, 3}; FF{DABC,13, 7}; FF{CDAB,14,11}; FF{BCDA,15,19};

/* Round 2 -- Let "GG{abcd,r,s}" denote the G-compression statement
           a = (a + G(b,c,d) + R[r] + Q[2]) <<< s
   and invoke it 16 times as follows: */
GG{ABCD, 0, 3}; GG{DABC, 4, 5}; GG{CDAB, 8, 9}; GG{BCDA,12,13};
GG{ABCD, 1, 3}; GG{DABC, 5, 5}; GG{CDAB, 9, 9}; GG{BCDA,13,13};
GG{ABCD, 2, 3}; GG{DABC, 6, 5}; GG{CDAB,10, 9}; GG{BCDA,14,13};
GG{ABCD, 3, 3}; GG{DABC, 7, 5}; GG{CDAB,11, 9}; GG{BCDA,15,13};

/* Round 3 -- Let "HH{abcd,r,s,t}" denote the H-compression statement
           a = (a + H(b,c,d) + R[r] + Q[3]) <<< s
   and invoke it 16 times as follows: */
HH{ABCD, 0, 3}; HH{DABC, 8, 9}; HH{CDAB, 4,11}; HH{BCDA,12,15};
HH{ABCD, 2, 3}; HH{DABC,10, 9}; HH{CDAB, 6,11}; HH{BCDA,14,15};
HH{ABCD, 1, 3}; HH{DABC, 9, 9}; HH{CDAB, 5,11}; HH{BCDA,13,15};
HH{ABCD, 3, 3}; HH{DABC,11, 9}; HH{CDAB, 7,11}; HH{BCDA,15,15};

/* Output state <A",B",C",D"> = <A',B',C',D'> + <A,B,C,D>. */
A" = A'+A; B" = B'+B; C" = C'+C; D" = D'+D;

Output

Finally, the message digest, MD4(M), is defined to be the final quadword state resulting from the above algorithm, after the outer loop completes (it begins with the low-order byte of A´, and ends with the high-order byte of D´): 

 

MD4(M) = <A', B', C', D'>;

This completes the description of MD4.

MD5

This section specifies MD5, one of the "cryptographic" checksum mechanisms employed in this specification.

Note:
This section is based on, and (unless stated otherwise) is technically aligned with, the Internet document RFC 1321, by R. Rivest, dated April 1992. However, for editorial reasons, this section stands independently, and no familiarity with that document is required. (Thus, the part of this section that duplicates information in the cited document is intended to be technically equivalent to that document, rewritten for the expository purposes of this document, and any technical discrepancies between the two are inadvertent and to be reconciled.)

MD5 is described by an algorithm that takes as input a bit-message M of arbitrary length and produces as output a 128-bit message digest (or hash, checksum, checksumtext, fingerprint) of M. MD5 is a non-invertible ("one-way") function, and it is claimed that it has the cryptographic property of being collision-resistant (or collision-"proof"): it is computationally infeasible to exhibit (that is, to produce, generate or construct) two distinct messages having the same message digest as one another, or to exhibit a single message having a given prespecified message digest. More precisely, it is claimed that the "difficulty" (computational complexity) of exhibiting two distinct messages having the same message digest has average order O(½·264), and that the difficulty of exhibiting a single message having a given message digest has average order O(½·2128).

Let M = <m0, ···, mn-1> be an arbitrarily given bit-message (sequence) of length n bits. Here n is an arbitrary non-negative integer (it may be 0, it need not be congruent to 0 (mod 8), and it may be arbitrarily large). Then the algorithm below is performed to compute the message digest of the message M, which is denoted by MD5(M).

For the remainder of this section, the little/big-endian identification of integers and 32-bit vectors is used (as defined in Mapping Mixed Bit/Byte-Sequences to Integers ).

Some Special Functions

The following four special functions are defined for use in the MD5 algorithm. Let U, V, W be 32-bit vectors (or, what amounts to the same given the fixing of the little/big endian correspondence in the remainder of this section, integers in the range [0, 232-1]).

Note:
As with the functions E and H (see Some Special Functions ), the functions G and I act in "bitwise parallel".

Append Padding Bits

The message M is padded (appended to), to produce a new bit-message of bit-length n´ = lambda(M´) > n and n´ equivalence 448 (mod 512) . This is performed as described in Append Padding Bits .

Append Length

The padded message M´ is appended with the 64-bit representation of n (mod 264), to produce the new bit-message of bit-length n´´ = lambda(M´´) = n´ + 64. This is performed as described in Append Length .

Note:
In the actual usage of MD5 as specified in DCE (namely, in Protected RPC), all messages actually protected with MD5 have length < 264 (see Protected RPC , and the referenced Open Group DCE 1.1 RPC Specification).

Initialise State Buffer and Trigonometric Vector

A quadword (= 128 bits) (external) state buffer, denoted <A´, B´, C´, D´>, is used to describe the pseudocode computation below. Here, each of A´, B´, C´, D´ is a word-sized variable. These variables are initialised to the same initialisation values or seeds as described in Initialise State Buffer and Trigonometric Vector .

The following array of 64 "trigonometric" (unsigned) words, T[0], ···, T[63] is further initialised: 

 

T[] = {0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
       0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
       0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
       0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
       0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
       0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
       0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed,
       0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
       0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
       0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
       0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
       0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
       0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039,
       0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
       0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
       0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};
Note:
The origin of the name "trigonometric" comes from the fact that T[i] = [232|sin(i+1)|], where on the right hand side "[···]" denotes the integral part of a real number, "|···|" denotes absolute value, and "sin" is the usual trigonometric sine function, whose arguments ("angles") i+1 are measured in radians. The values T[0], ···, T[63] are chosen for use in the MD5 algorithm because the bits of these 64 values are statistically well-distributed for this application.

Compress Message in 16-Word Chunks

Perform the following algorithm (expressed in pseudocode).

Its outer loop processes the padded, appended message M´´ in chunks of 16 words (= 512 bits) as follows: 

 

for (i = 0; i <= N/16 - 1; i += 1) {
        <A',B',C',D'> =
            COMPRESS(A',B',C',D',M"[16*i+0],···,M"[16*i+15]);
}

Its inner compression function, denoted COMPRESS(A´, B´, C´, D´, R[0], ···, R[15]), takes as input a 128-bit state vector <A´, B´, C´, D´> and a 512-bit message chunk <R[0], ···, R[15]>, and produces as output a 128-bit state vector, say <A´´, B´´, C´´, D´´>. It is defined by the following algorithm (consisting of 4 rounds of 16 compression operations each), where "+" denotes ("unsigned") addition (mod 232), and where F, G, H and I are the special functions defined in Some Special Functions : 

 


/* Initialise internal state buffer <A,B,C,D> = <A',B',C',D'>. */
A = A'; B = B'; C = C'; D = D';

/* Round 1 -- Let "FF{abcd,r,s,t}" denote the F-compression statement
           a = b + ((a + F(b,c,d) + R[r] + T[t]) <<< s)
   and invoke it 16 times as follows: */
FF{ABCD, 0, 7, 0}; FF{DABC, 1,12, 1}; FF{CDAB, 2,17, 2}; FF{BCDA, 3,22, 3};
FF{ABCD, 4, 7, 4}; FF{DABC, 5,12, 5}; FF{CDAB, 6,17, 6}; FF{BCDA, 7,22, 7};
FF{ABCD, 8, 7, 8}; FF{DABC, 9,12, 9}; FF{CDAB,10,17,10}; FF{BCDA,11,22,11};
FF{ABCD,12, 7,12}; FF{DABC,13,12,13}; FF{CDAB,14,17,14}; FF{BCDA,15,22,15};

/* Round 2 -- Let "GG{abcd,r,s,t}" denote the G-compression statement
           a = b + ((a + G(b,c,d) + R[r] + T[t]) <<< s)
   and invoke it 16 times as follows: */
GG{ABCD, 1, 5,16}; GG{DABC, 6, 9,17}; GG{CDAB,11,14,18}; GG{BCDA, 0,20,19};
GG{ABCD, 5, 5,20}; GG{DABC,10, 9,21}; GG{CDAB,15,14,22}; GG{BCDA, 4,20,23};
GG{ABCD, 9, 5,24}; GG{DABC,14, 9,25}; GG{CDAB, 3,14,26}; GG{BCDA, 8,20,27};
GG{ABCD,13, 5,28}; GG{DABC, 2, 9,29}; GG{CDAB, 7,14,30}; GG{BCDA,12,20,31};

/* Round 3 -- Let "HH{abcd,r,s,t}" denote the H-compression statement
           a = b + ((a + H(b,c,d) + R[r] + T[t]) <<< s)
   and invoke it 16 times as follows: */
HH{ABCD, 5, 4,32}; HH{DABC, 8,11,33}; HH{CDAB,11,16,34}; HH{BCDA,14,23,35};
HH{ABCD, 1, 4,36}; HH{DABC, 4,11,37}; HH{CDAB, 7,16,38}; HH{BCDA,10,23,39};
HH{ABCD,13, 4,40}; HH{DABC, 0,11,41}; HH{CDAB, 3,16,42}; HH{BCDA, 6,23,43};
HH{ABCD, 9, 4,44}; HH{DABC,12,11,45}; HH{CDAB,15,16,46}; HH{BCDA, 2,23,47};

/* Round 4 -- Let "II{abcd,r,s,t}" denote the I-compression statement
           a = b + ((a + I(b,c,d) + R[r] + T[t]) <<< s)
   and invoke it 16 times as follows: */
II{ABCD, 0, 6,48}; II{DABC, 7,10,49}; II{CDAB,14,15,50}; II{BCDA, 5,21,51};
II{ABCD,12, 6,52}; II{DABC, 3,10,53}; II{CDAB,10,15,54}; II{BCDA, 1,21,55};
II{ABCD, 8, 6,56}; II{DABC,15,10,57}; II{CDAB, 6,15,58}; II{BCDA,13,21,59};
II{ABCD, 4, 6,60}; II{DABC,11,10,61}; II{CDAB, 2,15,62}; II{BCDA, 9,21,63};

/* Output state <A",B",C",D"> = <A',B',C',D'> + <A,B,C,D>. */
A" = A'+A; B" = B'+B; C" = C'+C; D" = D'+D;

Output

Finally, the message digest, MD5(M), is defined to be the final quadword state resulting from the above algorithm, after the outer loop completes (it begins with the low-order byte of A´, and ends with the high-order byte of D´): 

 

MD5(M) = <A', B', C', D'>;

This completes the description of MD5.

Please note that the html version of this specification may contain formatting aberrations. The definitive version is available as an electronic publication on CD-ROM from The Open Group.

Contents Next section Index