1.1 Objective

The objective of the Risk Analysis (O-RA) Standard is to enable risk analysts to perform effective information security risk analysis using the Open FAIR™ framework. When coupled with the Risk Taxonomy (O-RT) Standard, it provides risk analysts with the specific processes necessary to perform effective risk analysis.

This document should be used with the companion O-RT Standard to:

• Educate information security, risk, and audit professionals
• Establish a common language for the information security and risk management profession
• Introduce rigor and consistency into analysis, which sets the stage for more effective risk modeling
• Explain the basis for risk analysis conclusions
• Strengthen existing risk assessment and analysis methods
• Create new risk assessment and analysis methods
• Evaluate the efficacy of risk assessment and analysis methods
• Establish metric standards and data sources

1.2 Overview

This document is intended to be used with the O-RT Standard, which defines the Open FAIR taxonomy for the factors that drive information security risk. Together, these two standards comprise a body of knowledge in the area of quantitative risk analysis.

Although the terms “risk” and “risk management” mean different things to different people, this document is intended to be applied toward the problem of managing the frequency and magnitude of loss that arise from a threat (whether human, animal, or natural event). In other words, managing “how often bad things happen, and how bad they are when they occur”.

Although the concepts and standards within this document were not developed with the intention of being applied towards other risk scenarios, experience has demonstrated that they can be effectively applied to other risk scenarios. For example, they have been successfully applied in managing the likelihood and consequence of adverse events associated with project management or finance, in legal risk, and by statistical consultants in cases where probable impact is a concern (e.g., introducing a non-native species into an ecosystem).

1.3 Conformance

Refer to The Open Group website for conformance requirements for this document.

1.4 Normative References

The following standards contain provisions which, through references in this document, constitute provisions of the Risk Analysis (O-RA) Standard. At the time of publication, the editions indicated were valid. All standards are subject to revision, and parties to agreements based on this standard are encouraged to investigate the possibility of applying the most recent editions of the standards listed below. Members of IEC and ISO maintain registers of currently valid International Standards.

• Risk Taxonomy (O-RT) Standard, Version 3.0.1, The Open Group Standard (C20B), November 2021, published by The Open Group; refer to: www.opengroup.org/library/c20b

1.5 Terminology

For the purposes of this document, the following terminology definitions apply:

Can Describes a possible feature or behavior available to the user or application.

May Describes a feature or behavior that is optional. To avoid ambiguity, the opposite of “may” is expressed as “need not”, instead of “may not”.

Shall Describes a feature or behavior that is a requirement. To avoid ambiguity, do not use “must” as an alternative to “shall”.

Shall not Describes a feature or behavior that is an absolute prohibition.

Should Describes a feature or behavior that is recommended but not required.

Will Same meaning as “shall”; “shall” is the preferred term.

1.6 Future Directions

As a standards body, The Open Group aims to evangelize the use of the Open FAIR method within the context of these risk assessment or management frameworks. Our aim is to continue to work to describe how the Open FAIR method may be used with other risk assessment frameworks. In doing so, The Open Group becomes not just a group offering yet another risk assessment framework, but a standards body which solves the difficult problem of developing consistent, defensible statements concerning risk.

For the Open FAIR Glossary, see the definitions in The Open Group Standard for Risk Taxonomy (O-RT), Version 3.0.1; accessible at: www.opengroup.org/library/c20b. Merriam-Webster’s Collegiate Dictionary[1] should be referenced for terms not defined in this section.

3.1 Risk Analysis Approach

All risk analysis approaches must include the following fundamental process elements:

• An effort to clearly identify and characterize the assets, threats, controls, and impact/loss elements at play within the risk scenario being assessed
• An understanding of the organizational context for the analysis; i.e., what is at stake from an organizational perspective, particularly with regard to the organization’s leadership perspective
• Measurement and/or estimation of the various risk factors
• Calculation of risk

The first two elements above can be summarized as “scoping” the analysis – scoping is the process of identifying a countable, easily understandable Loss Event and risk scenario statement. Practitioners must recognize that time spent in scoping is crucial to performing effective analyses. In fact, carefully scoping an analysis reduces time spent on the analysis due to better clarification of data requirements and less time spent troubleshooting and revising the analysis. More information on scoping the analysis appears in the Open FAIR Risk Analysis Process Guide (see Referenced Documents).

Risk-related data is never perfect. In other words, there will always be some amount of uncertainty in the values being used. As a result, measurements and estimates of risk factors should faithfully reflect the quality of data being used. The most common approach to achieving this is to use ranges and/or distributions rather than discrete values as inputs; by using ranges and/or distributions for measurements and estimates of risk factors, an Open FAIR risk analysis reflects that there is uncertainty about the future and that the data is always imperfect/incomplete. Therefore, Open FAIR analysts use Monte Carlo or other stochastic methods to calculate results.

3.2 Assessment versus Analysis

Many information security standards and frameworks specify that information risk assessments should be done but leave it to organizations to determine how to do them based on industry guidance. Moreover, the information security profession (and the broader enterprise risk management discipline to some degree) often does not clearly and consistently differentiate between “risk assessment” and “risk analysis”. There is a difference, however: risk assessments tend to encompass a broader context that includes processes and technologies that identify, evaluate, and report on risk-related concerns, while risk analyses use measurements and estimates of risk factors to provide an overall statement on the probable frequency and probable magnitude of future loss.

This distinction in the Open FAIR method between risk assessment and risk analysis is consistent with other standards, and the O-RT and O-RA Standards along with guidance documentation from The Open Group provide a way to quantify risk in those information security standards and frameworks. Practitioners who must perform information technology risk assessments to comply with other industry and regulatory standards, frameworks, and methodologies can therefore use the Open FAIR taxonomy and framework to build consistent and defensible risk statements that are measured in the same economic terms as other risks they have to manage.

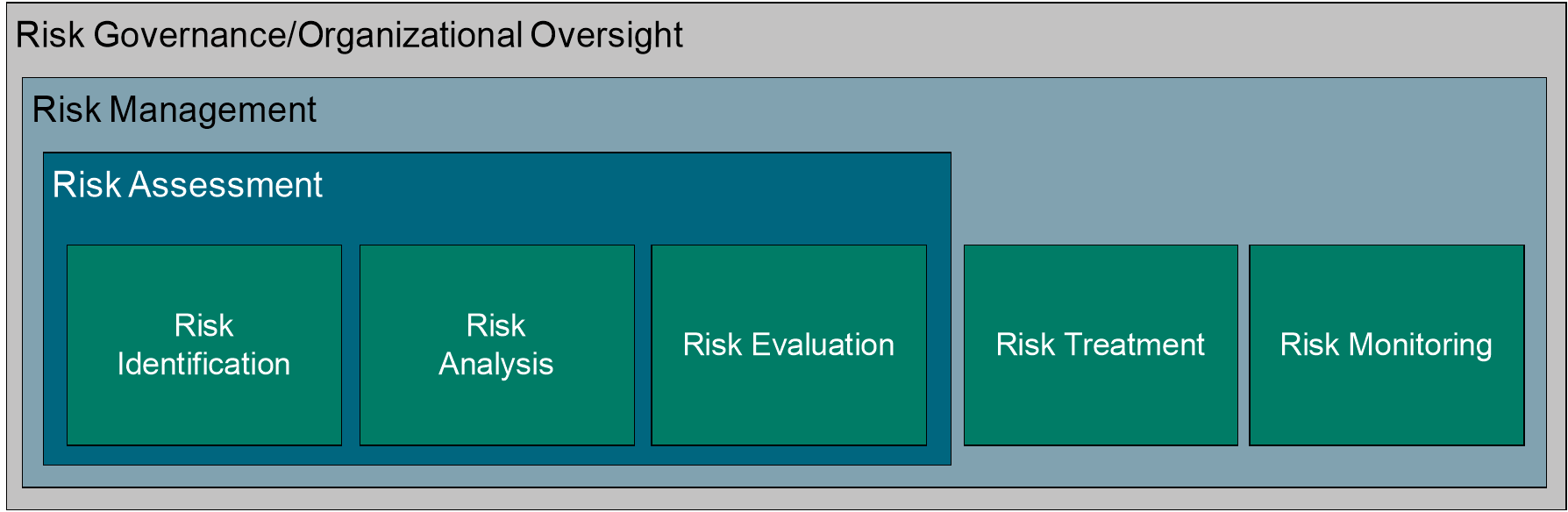
Figure 1: Risk Analysis in Context

3.3 Why is a Tightly-Defined Taxonomy Critical?

Without a logical, tightly-defined taxonomy, risk analysis approaches will be significantly impaired by an inability to measure and/or estimate risk factors. This, in turn, means that management will not have the necessary information for making well-informed comparisons and choices, which will lead to inconsistent and often cost-ineffective risk management decisions. The O-RT Standard provides the clear definition of Open FAIR risk factors and risk factor relationships necessary to guide professionals in their analysis of risks.

To measure risk, analysts incorporate into models what they believe they know about the future (certainty) and what they do not or cannot know (uncertainty) to estimate what will actually happen, and to estimate the range of outcomes of that future. The O-RT Standard describes the risk factors and structure of a model that estimates the likelihood of foreseeable losses due to information system-related events. Model providers build models using those risk factors as defined in the taxonomy to make accurate estimates of future outcomes.

All models at some level are “wrong”. Models, whether based upon human judgment and experience alone, scientific theory, mathematical equations, artificial intelligence, or a combination of all these, are limited in their ability to specifically and exactly predict the future; an outcome that cannot be determined with complete precision before it actually occurs and is observed.

The best an analyst can do is estimate risk factors and apply them through an accurate model, and even then, the model’s estimate of probable future loss may not include the actual future outcome when it occurs; the model or the estimates may have been inaccurate. However, modeling an uncertain future is the best humanity can do. The analyst must use the best available, current information to make informed probabilistic statements about what they believe may occur. (Indeed, human brains do this every moment.)

Analysts must identify and apply the knowledge they have and, at the same time, incorporate the uncertainty of what is not known – or not knowable. Some of that unknown may be discoverable through additional research. Other uncertainty, the uncertainty of a strictly unpredictable future outcome, cannot be discovered. Analysts – using all the information they have available – apply what measurements of risk factors are known, estimate risk factors that are unknown, and use risk models to estimate the frequency and magnitude of foreseeable future outcomes.

4.1 Key Foundational Concepts: Accuracy, Precision, Subjectivity, and Objectivity

Accurate forecasting of probable future loss from a given scenario requires an accurate estimation of risk factors. When modeling under conditions of uncertainty, it is best to value accuracy over precision and to report a range of values within which the actual value falls rather than to report an overly precise estimate that has little chance of being accurate.

Estimates informed by objective information (actual data, even if it is an estimate or industry-standard data when data individualized to a particular company is not available to the analyst) are more likely to be accurate than those informed solely or predominantly by subjective gut feelings and plagued with unstated biases or assumptions.

4.1.1 Accuracy versus Precision

An estimate of an uncertain future outcome is accurate when the observed future event is found to lie within the original estimate’s range. The accuracy of an estimate is binary: accurate or inaccurate. When observed in the future, the event either lies within the estimated range, or it does not.

The precision of an estimate is its range. Estimates that are too precise – that is, with a range that is too narrow, ignoring or minimizing the expression of uncertainty – can mislead decision-makers into thinking that there is more rigor in the risk analysis than there is. Using distributions and ranges increases the probability that an estimate is accurate. To increase the probability that an estimate is accurate, reduce its precision.

An example of an estimate that is precise but inaccurate would be an estimate that the wingspan of a Boeing™ 787 is exactly 107 feet. An example of an estimate that is accurate but not usefully precise would be an estimate that the wingspan of a Boeing 787 is between 1 foot and 1,000 feet.

An estimate is usefully precise when more precision would not improve or change the decision made by stakeholders. To extend the airplane wingspan example, if its wingspan is estimated to between 10 feet to 300 feet, and if the objective of the estimation exercise is to inform the builder of a hangar how large it should be to cost-effectively house the plane, then the estimate is likely accurate, but it is not usefully precise to support an economically efficient hangar construction project.

To provide high-quality estimates that stakeholders can use to make effective decisions, analysts must first ensure they are accurate. To improve the usefulness of the estimate, analysts shall provide as much precision as the research, data, and reasoning of that estimate can support, while keeping the estimate accurate.

Risk analysis results cannot be more precise than the input values. The number of significant digits resulting from multiplication is the same as the number of significant digits in the least precise input (i.e., have no more non-zero significant digits). In other words, analysts should not represent more precision in an analysis than the data going into it can support.

4.1.2 Subjectivity versus Objectivity

All measurements lie on a spectrum ranging from the purely subjective to purely objective but, in reality, no measurement is perfectly objective because humans are inherently subjective. Analysts must decide what data to capture, how to collect it, and what filters to apply when using and presenting it, all of which can (and frequently do) introduce bias.

Highly subjective measurements of risk factors are those which are strongly influenced by personal feelings, interpretations, prejudice, or a simple lack of subject matter knowledge.

Highly objective risk measurements of risk factors are those which are not influenced by personal feelings, interpretations, or prejudice, but which are supported by facts, observations, and evidence upon which impartial observers would agree. The analyst should make measurements as objective as is practical and useful to the analysis at hand.

To increase the objectivity of this risk measurement, the analyst has two primary approaches. The first is to gather more data to help inform the risk estimate. The second is to better understand how the estimates are derived – in other words, to better define and apply the factors that make up or influence the estimates. The precise definitions and relationships provided in the O-RT Standard help to inform this understanding.

For example, if an analyst asked a random employee at a company how many laptops the company loses in a given year, that employee’s opinion would be a comparatively subjective answer, perhaps informed only by their own experience or knowledge of co-workers who have lost laptops. To improve the objectivity of the lost laptop measurement, that analyst could go to the IT group in charge of managing IT assets and ask for the records of lost laptops for the past several years. Impartial stakeholders would commonly accept the accuracy and precision of these records and would interpret them in the same way, making these measurements more objective and agreed upon as true compared to one random employee’s opinion or personal history of laptop loss.

4.2 What is an Estimate?

Estimating involves calculating roughly and usually requires using imperfect data. Analysts use statistical concepts to quantify or specify estimates of an uncertain, unknowable-in-advance future outcome. The essential elements of every estimate are its range, most likely value and distribution.

4.2.1 The Range of the Estimate Determines Its Accuracy

Estimates have a minimum and maximum value that specifies their range. An estimate is accurate when the outcome measured in the future is found to be located within that range.

Because the future is uncertain and estimation models are imperfect representations of the complex natural world, a modeled estimate will be inaccurate some of the time: estimates have a probability of being accurate. That probability can be increased at the expense of the estimate’s precision. In other words, increasing an estimate’s range increases the probability of it being accurate but comes at the expense of reduced precision of that estimate.

At some point, although accurate, an imprecise estimate is no longer useful. The practical tradeoff made in this document is that estimates should be accurate 90% of the time. This probability of accuracy makes a tradeoff between the probability of the estimate being accurate for improved precision.

To accomplish this accuracy-precision tradeoff, the analyst should have a degree of belief that the materialized, observed future outcome will not be below the estimate’s minimum more than one time out of 20, or 5% of the time. Similarly, the analyst should have a degree of belief that the materialized, observed future outcome will not be above the estimate’s maximum value more than one time out of 20, or again 5% of the time.

4.2.2 Standardizing on Most Likely Value as a Way of Estimating Risk Factors

The Open FAIR model characterizes statistical distributions though common, intuitive constructions of the minimum, maximum, and most likely values of the distribution. Analytic tools can then convert these standard parameters into specific ones required by the distribution chosen by the analyst.

The most likely value is the peak of the distribution, sometimes called the mode in a discrete distribution, other times simply the peak of a continuous one. In the context of inputs into the Open FAIR model, when making an estimate for a factor of a risk model, the most likely value represents the value within the range believed to have the highest probability of being the true value when observed in the future.

For instance, an analyst estimates a given Loss Event to occur with a probable frequency of between 1 and 20 times over the next year and has historical evidence over many years suggesting that 11 or 12 of these Loss Events is more probable than 1, 2, 19, or 20. As a result, the analyst would select 11 or 12 as the “most likely value”, increasing its probability relative to the other values in the range. The degree to which 12 Loss Events is believed more probable than other values in the range is reflected in how much the probability of the most likely value is increased relative to the other values within the range.

4.2.3 Specifying an Estimate’s Distribution Improves Its Precision

Analysts can improve the usefulness and precision of the estimate by selecting a statistical distribution bounded by the accurate range described above that best reflects what they know about the risk factor being modeled. In other words, by deliberately choosing a distribution, an analyst is using knowledge about the risk factor being estimated to model their degree of belief that some outcomes are more likely than others within the specified range of the estimate. For instance, distributions for which analysts have a very high degree of belief in the most likely value will be very peaked and narrow; flatter distributions indicate that analysts have a low degree of belief that the most likely value is all that likely compared to others within the range.

If the risk analyst knows nothing about an estimate aside from its accurate minimum and maximum values, they would choose the uniform distribution – such a choice indicates complete uncertainty about the likelihood of the modeled, estimated future outcome aside from its minimum and maximum range values. If the risk analyst knows that a modeled potential loss has the potential of a “fat tail”, they would choose a log-normal statistical distribution. Similarly, the analyst may know that the Threat Event Frequency is best modeled through Poisson distribution.[2]

Note: The Open FAIR model is agnostic on what distribution is “right”. Instead, analysts shall use their best knowledge of that risk factor and what additional information they know about it to select the most appropriate distribution. The Open FAIR model is also agnostic on any required distribution choices that a risk model or calculating tool provides to the risk analyst. From an Open FAIR standard conformance or compliance standpoint, there are no minimum requirements placed upon tool or model suppliers to include or exclude any statistical distribution available for the analysts to use in modeling any risk factor.

4.3 The Calibration Technique to Develop Accurate Estimates

Calibration allows an individual to make better estimates. Because measuring risk involves making good estimates, calibration is critical for risk analysts to understand. Performing calibration to make better estimates is a skill that can be learned.

4.3.1 Starting with the Absurd

Calibration starts with making absurd estimates. Beginning by making absurd estimates enables the risk analyst to recognize starting values for the estimation that are clearly not possible. It also assists in breaking any bias that an analyst may have.

To extend the Boeing 787 wingspan estimate example from earlier, an analyst might initially estimate the wingspan with an absurdly wide range of 10 feet on the low side and 300 feet on the high side. Someone with experience seeing the airplanes at airports will recognize that these values are absurd estimates, perhaps using as frames of reference the height of a basketball hoop on the low end and the length of a football field on the high end. Once the analyst understands how absurd these values for minimum and maximum (min/max) in the range are, they can start to narrow in on more appropriate min/max values in a range to support the decision at hand.

Starting with these clearly absurd values leads to more accurate estimates, reduces the likelihood of an inaccurate estimate, and makes it more possible to narrow in on a more realistic range of min/max values.

4.3.2 Decomposing the Problem

Measurement and estimation in risk analysis requires the analyst to decompose broad, high-level risk components into smaller pieces that are easier to deal with. An example of this might be trying to estimate the height of the Willis Tower in Chicago. By decomposing the problem into “How many floors tall is the building?” and “How much vertical space does each floor occupy?” the analyst can start to make sense of the entire question.

In information security risk analysis, a similar broad question might be, “How much risk does this firm have around lost laptops and Personally Identifiable Information (PII)?” To decompose this into components that can be more easily dealt with (and for which there is data to support a risk analysis), the analyst can ask themselves questions such as, “How many laptops have we historically lost each year? How much PII is being stored on laptops by employees? What costs do organizations similar to ours experience when they lose PII?”

4.3.2.1    Making Estimates with Incomplete or Very Little Information

Analysts almost always have to work with the information they have, not the information they want. Analysts have several approaches they can take to make calibrated, accurate estimates with missing or incomplete information. The main point is this: analysts have more information than they think, but they must be creative in how to discover and use what they have. Enrico Fermi developed techniques to do this, and the literature around “Fermi Problems” is referenced in the example below.

Suppose an analyst had to estimate the number of plays attributed to William Shakespeare. An analyst who had a copy of the complete works at home and had appeared in a handful of Shakespeare plays may not need to decompose that value into its factors. Based upon that unique knowledge and experience, the analyst could estimate Shakespeare’s lifetime production between “20 to 40 plays” with relative ease.

Someone else, however, without access to that knowledge and experience and who has no idea of Shakespeare’s lifetime achievement could treat “the number of plays attributed to Shakespeare” as a Fermi Problem and derive it from the sub-factors “number of years of productivity” and “number of plays per year”. Without direct knowledge of Shakespeare but with some knowledge of Elizabethan times and the productivity of playwrights, a productive lifetime of “10 to 30 years” and a playwright productivity of “one to three plays per year” could be reasonably estimated and, when combined, would lead to an estimated lifetime achievement of between 10 to 90 plays. For this analyst, who has not trodden the boards as Benvolio, decomposing a difficult-to-estimate value into easier-to-estimate factors for which more data/rationale was readily available, deriving an accurate estimate becomes possible. If that estimate still were not usefully precise, the analyst could further research the sub-factors to refine their precision. For example, the analyst could quickly research Shakespeare’s age at death to narrow the estimate of productive lifetime.

The same is true when estimating risk factors in Open FAIR models. If one factor is difficult to estimate given the available information, the analyst should research information that informs accurate estimates of its sub-factors, ultimately producing an accurate estimate of the factor in question.

4.3.3 Testing Confidence Using the Wheel, Establishing 90% Confidence Overall, and 95% Confidence at Each End

The wheel is a mechanism to help an analyst strengthen their conviction or confidence in an estimated range of values, to move them to a point where the analyst is 90% confident that the actual value observed in the future will lie within the min/max range; in other words, the estimate should have a 90% chance of being found accurate. The wheel mechanism helps risk analysts improve their calibration abilities by forcing them to evaluate (and revise) their choice for a min/max value in a range.

With an initial absurd range for the value, the next step is to narrow the range to more accurately estimate the actual values so that the analyst is confident that the actual value will fall within the range 90% of the time (a 90% confidence interval).

Douglas Hubbard (see Referenced Documents) uses the analogy of a wheel to help narrow the range. The analyst is offered a choice between two scenarios:

1. They will receive $1,000 if the actual value falls within their prediction.
2. Spinning a wheel with 90% of its area painted black and 10% painted red. They will win $1,000 if the wheel stops in the black.

The wheel implements a 90% confidence interval, and the desired goal is that the analyst has no preference between the two methods. An analyst who prefers the wheel is not confident that their estimate represents a 90% confidence interval for the value, which demands that estimate be revised; in fact, this analyst must have a degree of confidence less than 90% if they prefer the wheel, and they should make their estimated range wider. The confidence interval can be tightened by asking the analyst to make the same choice regarding whether the estimate will be less than (or greater than) the minimum (maximum) of the specified range 95% of the time.

4.3.4 Challenging Assumptions

To fill in missing information, analysts must make assumptions – those things analysts take to be true even if they are not. These assumptions could be for values in the Open FAIR risk analysis or about the relevant Threat Communities, to name a couple of examples. Assumptions may be challenged by considering other analysts’ estimates and by researching data that is useful to the estimation activity. Challenging assumptions helps prevent an inaccurate assumption from leading to an inaccurate estimate.

4.3.5 Range Confidence

Analysts improve their confidence in the accuracy of the range through training in calibration in removing personal estimating biases. The wheel exercise, described in Section 3.3.3, helps to improve calibration and reduce personal bias.

4.4 Using Monte Carlo Analysis

Monte Carlo simulation[3] is a method for modeling the future in the face of significant uncertainty to show the relative probabilities and impacts of future outcomes. By performing repeated sampling of random variables characterizing Open FAIR risk factors, Monte Carlo simulation models thousands of outcomes consistent with those parameters and their distributions to obtain a distribution of simulated annual losses. That output is used in risk analysis to show the probability distribution of likely outcomes of an uncertain future. The primary advantage of using a Monte Carlo simulation in risk analysis is that it portrays the full risk exposure story: it shows not only averages and most likely outcomes but also the entire range of estimated possible losses and their relative probability of occurrence.

The methodology standardized here is a basic one covering a foundational series of stages to define, scope, decompose, and quantitatively evaluate potential Loss Events in an information system.

• Stage 1: Identify the Loss Scenario (Scope the Analysis)
• Stage 2: Evaluate the Loss Event Frequency
• Stage 3: Evaluate the Loss Magnitude (LM)
• Stage 4: Derive and Articulate Risk
• Stage 5: Model the Effect of Controls

Throughout the risk analysis process, the risk analyst shall document key assumptions and the rationale for estimates used. Well-documented assumptions should include the reasoning for the assumption as well as any sources that contributed to them. A well-documented rationale should state the source of all estimates – the source may be systems (e.g., logs), groups (e.g., incident response), or industry data.

By documenting the key assumptions and rationale used, the analyst will be better able to defend the analysis and explain the results to decision-makers. This also allows analysts to compare approaches if results differ. Documenting the key assumptions and rationale used adds to the integrity of the analysis because analysts can demonstrate where they found data and why certain data was used for estimates in the analysis.

5.1 Stage 1: Identify the Loss Scenario (Scope the Analysis)

In this critical stage of the analysis, the “story of loss” is defined from a specific stakeholder’s perspective – the Primary Stakeholder, typically the owner of the identified Asset, is the one who bears and values the loss. The loss can be described as an event, and to analyze the probable future loss related to any given event/scenario, the analyst must have a clear understanding of what the scenario/event is from the perspective of the Primary Stakeholder.

The Loss Scenario is the story of that loss that forms a sentence:

A Threat Agent breaches or impairs an information Asset that causes an observable Loss Event that has direct economic consequences (Primary Loss) and may have economic consequences initiated by reactions from others (Secondary Loss).

Conceptually, a Loss Scenario looks like Figure 2.

Figure 2: Decomposing an Open FAIR Loss Scenario

To complete the Loss Scenario, the analyst must identify and define the Primary Stakeholder, the Asset, the Threat Agent/Community, the Threat Event, and the Loss Event.

5.1.1 Identify the Primary Stakeholder

The Primary Stakeholder is the individual or organization who owns or is accountable for the Asset that suffers lost measurable, economic value from a Loss Event.

5.1.2 Identify the Asset

The Asset is the information, information system, or information system component that is breached or impaired by the Threat Agent in a manner whereby its value is diminished or the act introduces liability to the Primary Stakeholder. Assets inherit value based on the business processes/organizational objectives they, or the data/applications that reside on or run using them, support.

5.1.3 Identify the Threat Agent/Community

The Threat Agent is the person, place, or thing capable of acting against the Asset in a way that results in a loss described in the Loss Scenario.

By examining the nature of the organization (e.g., the industry it is in) and the conditions surrounding the Asset (e.g., an HR executive’s office), the analyst can begin to classify the overall Threat Agent population into one or more Threat Communities that might reasonably apply. Including every conceivable Threat Community in the analysis is likely not a good use of time; instead, the analyst should identify the most probable Threat Communities for the Loss Scenario.

To further define a Threat Community, the analyst can build a “profile” or list of common characteristics associated with a given Threat Community. The Open FAIR model does not define a standard list of attributes to evaluate for each and every Threat Community. Rather, each organization should create a list of Threat Community attributes that can be reused across multiple risk analyses to ensure internal consistency. Common characteristics include:

• Motive
• Objective
• Access Method
• Personal Risk Tolerance
• Desired Visibility
• Sponsorship
• Skill Rating
• Resources

5.1.4 Identify the Threat Event

A Threat Event occurs when the Threat Agent acts against information Assets by attempting to breach or otherwise impair them to impact their confidentiality, integrity, or availability.

There are four types of Threat Events:

• Malicious (where harm is intended); e.g., an attempted theft
• Error (where an act occurred that was not intended); e.g., entering the wrong command at a keyboard
• Failure (where an act resulted in unintended consequences); e.g., the right command was given, but the system failed to perform as intended
• Natural (resulting from acts of nature); e.g., high winds

For each Threat Event type, the analyst can ask, “Who or what could potentially harm the Asset in this way?”. However, distinguishing between probable and merely possible Threat Events is crucial. By considering the nature of the Threat Communities relative to the industry, organization, and Asset, the analyst selects the reasonable, probable Loss Scenarios and avoids the speculative, highly improbable ones.

In many cases, a final consideration regarding the definition of a Threat Event under analysis is to identify the “threat vector”. The threat vector represents the path and/or method used by the Threat Agent to breach/impair the Asset, and each threat vector may have a different frequency and different control levels. For example, an attacker seeking to gain access to sensitive corporate information may try any of a number of vectors, such as technical attacks, leveraging human targets, etc.

5.1.5 Identify the Loss Event

The observable Loss Event is a confidentiality, integrity, or availability event that the stakeholder can observe and respond to. For a loss to occur, it first must be observed, for only an observable loss can be responded to and valued; a loss that has not yet been observed can be considered a Threat Event until the loss is observed.

Every Loss Scenario must have a direct consequence evaluated as the economic cost directly associated by the observed confidentiality, integrity, or availability loss of the Asset – this is the Primary Loss. The impact of that observable Primary Loss then must be evaluated in economic terms, measured in dollars, pounds, euros, yen, yuan, etc. All losses in the Open FAIR model are measured in these economic terms.

From that Primary Loss, there is a probability that Secondary Stakeholders will react, resulting in additional losses to the Primary Stakeholder – an additional loss resulting from the actions of Secondary Stakeholders is the Secondary Loss. For example, regulators, customers, or the media may react to the initial information system loss and initiate their own actions against Primary Stakeholder Assets, usually financial Assets.

Examples of Secondary Losses include consumer breach notification, regulatory reporting of the incident, lawsuits, or “bad press”, all intended to impact the Primary Stakeholder financially. At a minimum, the Primary Stakeholder’s response to these Threat Events represents a response cost in the Open FAIR model. Additional financial costs to the Primary Stakeholder may build from there.

5.1.6 Limiting the Scope of the Loss Scenario

Whether an analysis succeeds or not first depends upon whether its scope is sufficiently limited to be executed successfully. The scope of an analysis is too broad when it includes multiple Threat Communities that do not share common characteristics, multiple observable Loss Events, or multiple Asset types.

Performing a single analysis that encompasses more than one Threat Agent/Community or Asset is generally acceptable, but careful consideration should be given if those multiple Threat Agents/Communities have significantly different Threat Capabilities, attack the Asset through different threat vectors, or act against the Asset at significantly different frequencies. When any of these conditions occur, analysts should create multiple Loss Scenarios and analyze them separately.

Combining multiple observable losses (confidentiality, integrity, availability) together should be avoided. For example, the forms of losses associated with availability are likely to be very different from those associated with confidentiality or integrity. The Loss Magnitude of the forms of loss are likely to differ significantly, too. Trying to combine these into a single Loss Scenario adds needless complexity to the analysis and often distracts the analysis team from what matters most.

Finally, analysts should avoid combining different Asset types into a single analysis, for this often makes modeling Loss Event Frequency and Loss Magnitude harder than it would be if the Loss Scenarios were separated. For example, a Threat Agent who steals a laptop out of an employee’s car has both the laptop and the data on it. Combining the Loss Magnitude of both the laptop and data together may be much harder to do accurately than doing two analyses, one for the laptop hardware that needs to be replaced, and one for the loss associated with the data on the laptop.

Analyzing several, focused Loss Scenarios often takes less time and is more efficient than trying to make estimates for more complex scenarios.

The analysis is scoped after defining the Loss Scenario and all key, relevant assumptions have been made and documented.

Note: In any risk analysis, regardless of method, the analyst must make assumptions to fill in for missing, incomplete information. Analysts must clearly document their key assumptions to ensure all that those who review the analysis understand the basis for the values used and to assess whether the assumptions used are reasonable for the analysis.

In scoping the Loss Scenario, the Open FAIR risk factors are assumed to be independently identically distributed.

5.1.7 Decomposing the Loss Scenario

The analyst can now begin modeling the risk within the Open FAIR quantitative framework to evaluate the Loss Event Frequency and Loss Magnitude associated with this Loss Scenario.

Figure 3 shows the decomposition of a Loss Scenario and can be understood, from left to right, as showing the chain of events, beginning with a Threat Agent contacting an Asset and ending with the Loss Event(s). It will be decomposed further to show the Loss Event Frequency and Loss Magnitude components.

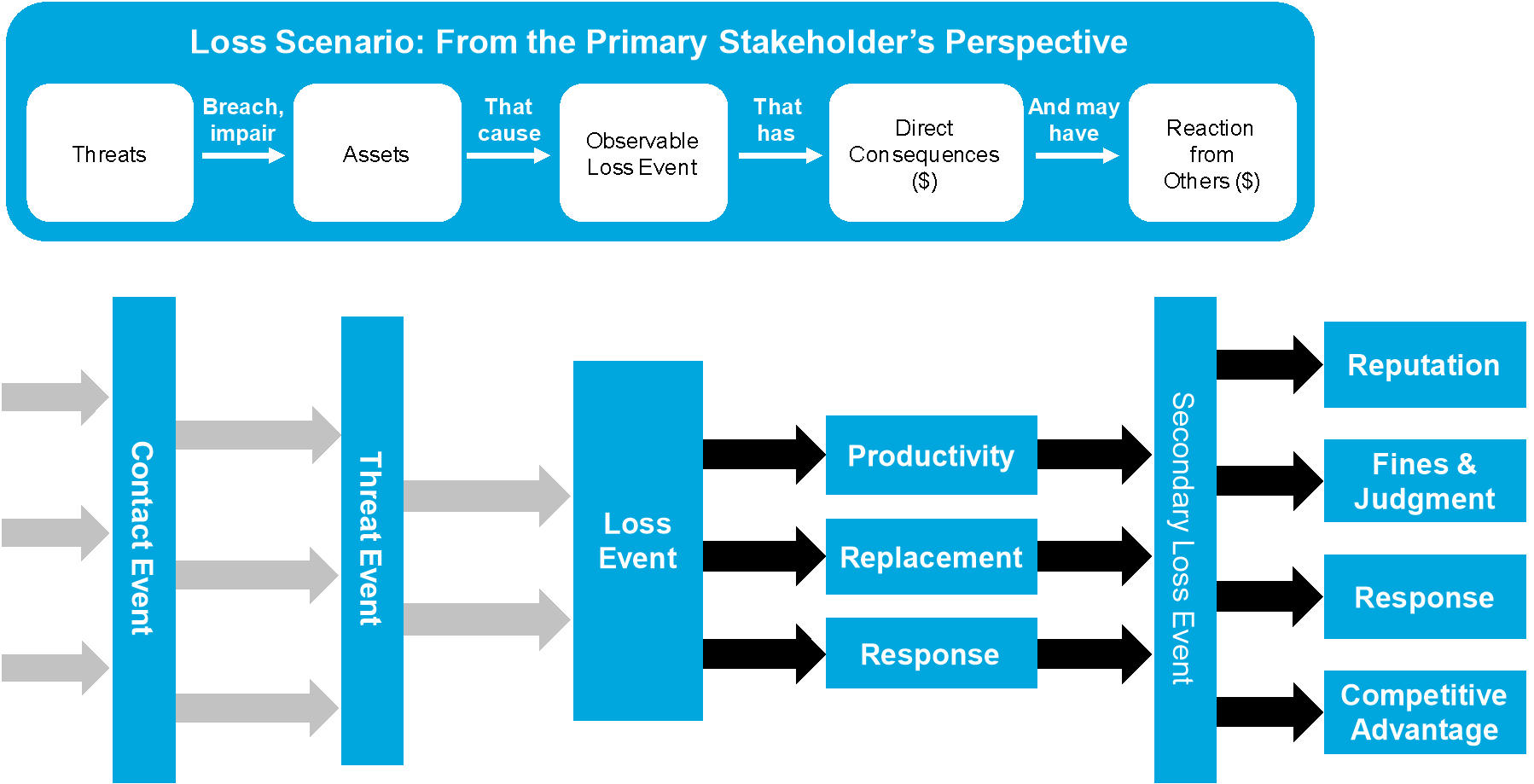
Figure 3: Decomposing an Open FAIR Loss Event

5.2 Stage 2: Evaluate the Loss Event Frequency

Having described the Loss Scenario, the analyst can begin collecting data and estimates for the various Open FAIR risk factors.

At the highest level, to understand the probable future loss associated with a given Loss Scenario, the analyst needs an estimate of how many times the Loss Scenario is likely to occur over a given timeframe – this is the Loss Event Frequency (LEF).

When estimating Loss Event Frequency, the analyst must choose which risk factors in the Open FAIR taxonomy to estimate. For example, is it better to estimate Loss Event Frequency than deriving that risk factor from its lower-level sub-factors by estimating Threat Event Frequency and Vulnerability? Should the analyst go even further down into in the Open FAIR taxonomy, decomposing those two risk factors into their sub-factors Contact Frequency (CF), Probability of Action (PoA), Threat Capability (TCap), and Resistance Strength (RS) to derive all the higher factors?

Analyses should be performed using the risk factors that have the highest quality of data to support accurate and usefully precise calibrated estimates. When possible, analysts should estimate factors at the highest level possible in the Open FAIR taxonomy. However, when an accurate estimate is not usefully precise and information is available that informs accurate and usefully precise estimates of lower-level risk factors, the analyst should decompose the higher-level risk factor into its component sub-factors and estimate them.

Analysts should not assume that they must always derive Loss Event Frequency from estimates of its lower-level factors, nor does it mean that it is always advantageous to do so. In fact, estimating factors lower in the model can involve increasing levels of abstraction and difficulty in many scenarios without improving the quality of the analysis.

Utilizing a top-down approach and working higher in the taxonomy offers increased efficiency and, when there is historical data supporting an estimate at the Loss Event Frequency level, can result in a more objective analysis. By leveraging a top-down approach, the analyst tries to accurately and sufficiently precisely estimate Loss Event Frequency, only decomposing it into its sub-factors if useful or necessary to serve the purpose of the analysis. The guiding principle is this: select risk factors that represent the simplest model possible that is accurate and usefully precise.

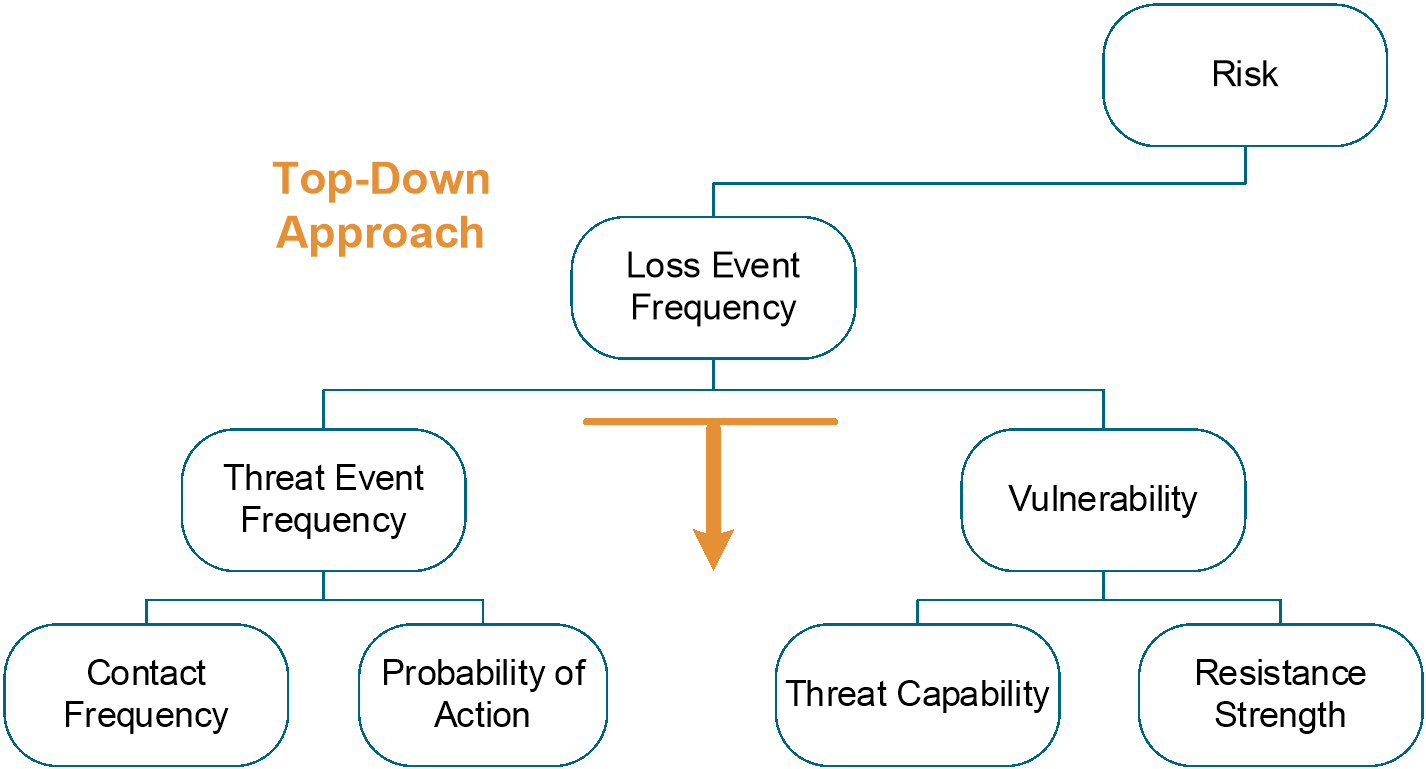
Figure 4: Top-Down Approach

5.2.1 Estimate the Loss Event Frequency

A Loss Event Frequency estimate reflects how many times the Loss Scenario is expected to occur in a given timeframe. If the Loss Event being measured has occurred in the recent past, the analyst may be able to estimate Loss Event Frequency directly.

If there is no data on prior Loss Events, if factors (such as Controls) have changed, or if there is better/more objective data about Threat Events than Loss Events, the analyst should step down one layer and attempt to work at the level of Threat Event Frequency (TEF) and Vulnerability (Vuln).

The purpose of the analysis will also determine the level of abstraction. For instance, if the analyst is evaluating several different Control options to determine which option is most effective from a risk reduction perspective, then deriving Vulnerability by analyzing Resistance Strength and Threat Capability may be most useful. In this way, the analyst can estimate the change in Resistance Strength due to the evaluated Control option.

If the analyst is unable to estimate the Loss Event Frequency directly, if factors have changed, if there is better/more objective data about Threat Events than Loss Events, or if the purpose of the analysis requires it, the analyst should estimate Threat Event Frequency and Vulnerability to derive the Loss Event Frequency.

5.2.1.1    Estimate the Threat Event Frequency

A Threat Event Frequency estimate reflects how many times the Threat Agent will attempt to breach or impair the Asset’s confidentiality, integrity, and/or availability. A Threat Event Frequency estimate would be based upon how frequently contact between the Threat Agent and the Asset occurs (the Contact Frequency) and the probability that the Threat Agent would act against the Asset (the Probability of Action).

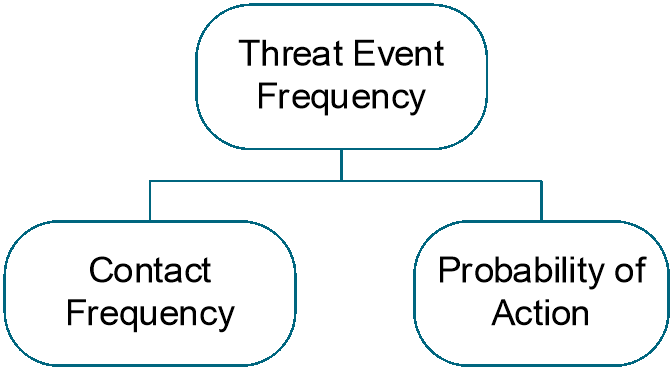
Figure 5: Threat Event Frequency

For a Loss Event to occur, a Threat Agent must first contact an Asset. After contacting the Asset, there is then a Probability of Action for whether the Threat Agent will then try to cause a Threat Event. However, if the Threat Agent does not act against the Asset despite making contact, no Threat Event occurs, so not every Contact Event results in a Threat Event.

The probability that the Threat Agent would act is driven by three primary factors that affect how the Threat Agent perceives the benefits of acting against the asset versus the costs of conducting the act against the asset:

• Perceived value of the Asset to them (based upon their motives – financial gain, revenge, etc.)
• Perceived level of effort required (i.e., how vulnerable the Asset appears to be)
• Perceived risk of being caught and suffering unacceptable consequences

Probability of Action is influenced by what the Threat Agent perceives or believes, and it is modeled in the Open FAIR framework as an economic analysis of costs and benefits of a successful attack to the Threat Agent. A Threat Agent would have a lower Probability of Action if the perceived payoff of a successful attack fell, the level of effort rose, or the consequences to the Threat Agent rose. Assuming all other things are equal, examples of reducing the Probability of Action include:

• Changing PII policies – if Threat Agents regularly contact a database and discover that the organization has changed its policies to reduce how much PII is stored in one location, their perceived value of the Asset has been reduced because they will be unable to obtain as much benefit from a successful attack
• Encrypting databases – if after contacting a database Threat Agents discover it is encrypted, the perceived level of effort to capture useful information from the database has risen compared to an unencrypted database, they will reduce their attempts to penetrate it
• Installing new surveillance cameras – if Threat Agents passing by an ATM discover new surveillance cameras installed around it and believe that their probability of being caught and prosecuted for robbery has increased, they will reduce how often they try to break into it

5.2.1.2    Estimate Vulnerability

Vulnerability, or its synonym susceptibility, is the probability that a Threat Event results in a Loss Event.

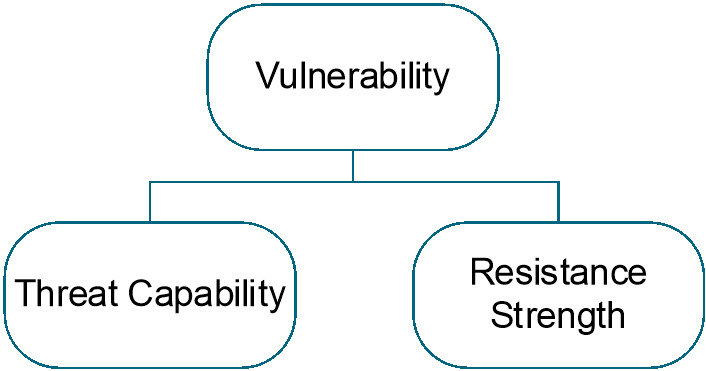
Figure 6: Vulnerability

If the analyst has data on Threat Events and Loss Events in a given timeframe, it is possible to estimate Vulnerability directly by comparing the number of successful Loss Events to the total Threat Events.

If the analyst lacks this data, Vulnerability can be estimated at the lower level by considering how the Threat Agent’s knowledge, skills, and resources (Threat Capability) compare to the Control environment around the Asset and the Primary Stakeholder’s ability to resist the Threat Agent’s actions (Resistance Strength).

Threat Agents vary in their capability: some are relatively easy to resist while others can penetrate the most heavily protected Asset. The Open FAIR model reflects the variability of a Threat Agent’s resources, skill, organization, and persistence as its Threat Capability. Threat Capability is measured as the percentile value representing the Threat Agent’s relative position on the distribution of potential attackers.

Attackers exist on a continuum of skills and resources, including at one end of the continuum attackers with little skill, little experience, and a low level of determination, and including on the other end attackers who are highly skilled, experienced, and determined. In performing an Open FAIR risk analysis, the analyst defines a minimum likely capability for the threat, a maximum likely value, and a most likely value. These represent the minimum level of skills expected for an attacker to have, the maximum level of skills an attacker might have, and the skill level of the most likely attacker. This skill level is relative to the threat vector used; for example, an attacker may be highly skilled at utilizing a particular threat vector but not at all skilled at utilizing a different threat vector.

The Threat Capability continuum describes attackers as existing at various percentiles, where the 25^th percentile of Threat Agents are less skilled and able than the 50^th percentile of Threat Agents who are less skilled and able than the 99^th percentile of Threat Agents.

To resist the Threat Agent’s capability, the Asset has Controls and protection against a Threat Agent’s capability, which contribute to the Asset’s Resistance Strength. Resistance Strength is the strength of a Control as compared to the probable level of force that a Threat Agent is capable of applying against an Asset, and it is measured as the percentile value representing the highest Threat Capability against which it could be successfully defended.

Note: Both Threat Capability and Resistance Strength are expressed in a range to account for increasing levels of abstraction and uncertainty involved with using the Threat Capability continuum.

The probability that a Threat Event will result in a Loss Event – or the percentage of Threat Events over a given timeframe that will result in Loss Events – is variable. Not all Assets of a given type are equally protected. For example, some Assets, such as user bank accounts, have stronger passwords than others, so an attack that fails against one user’s bank account with a comparatively strong password will succeed against another user’s account with a comparatively weaker password.

After estimating the ranges for Threat Capability and Resistance Strength, the analyst will use Monte Carlo analysis to compare a random sample from Threat Capability with a random sample from Resistance Strength and derive Vulnerability, the probability that the Threat Capability exceeds the Resistance Strength in any given threat action of the type being analyzed.

5.2.2 Decomposing Loss Event Frequency

Figure 7 shows the decomposition of Loss Event Frequency.

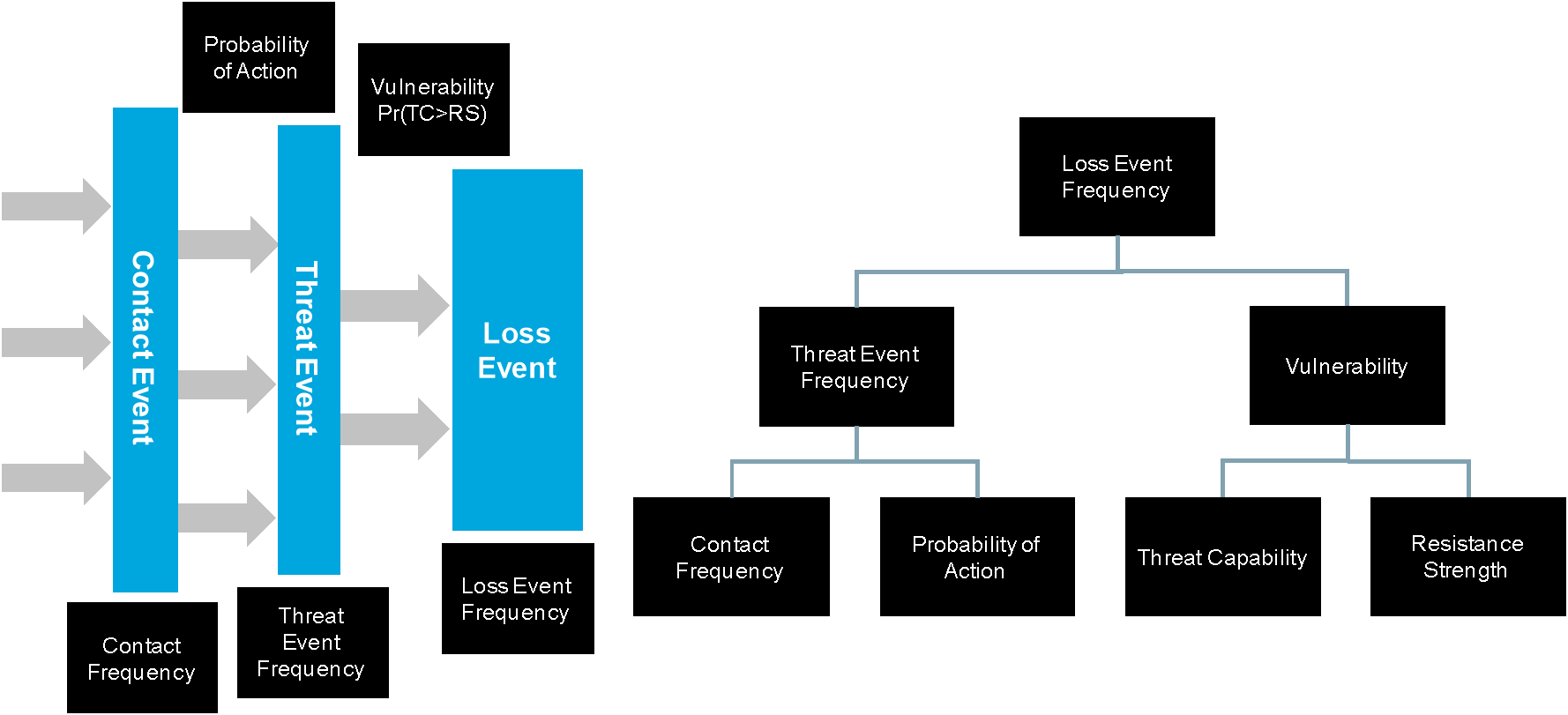
Figure 7: Decomposing Loss Event Frequency

By leveraging a top-down approach, the analyst will first try to estimate Loss Event Frequency itself if it is possible to make a defensible estimate, only decomposing it into its factors if useful or necessary for the purpose of the analysis or if the type and quality of data are better/more objective at the lower levels.

5.3 Stage 3: Evaluate the Loss Magnitude

After evaluating Loss Event Frequency, the analyst can evaluate Loss Magnitude – the total financial value lost when a Loss Event occurs – using the Open FAIR loss forms to help identify the Primary Loss(es) and any Secondary Loss(es).

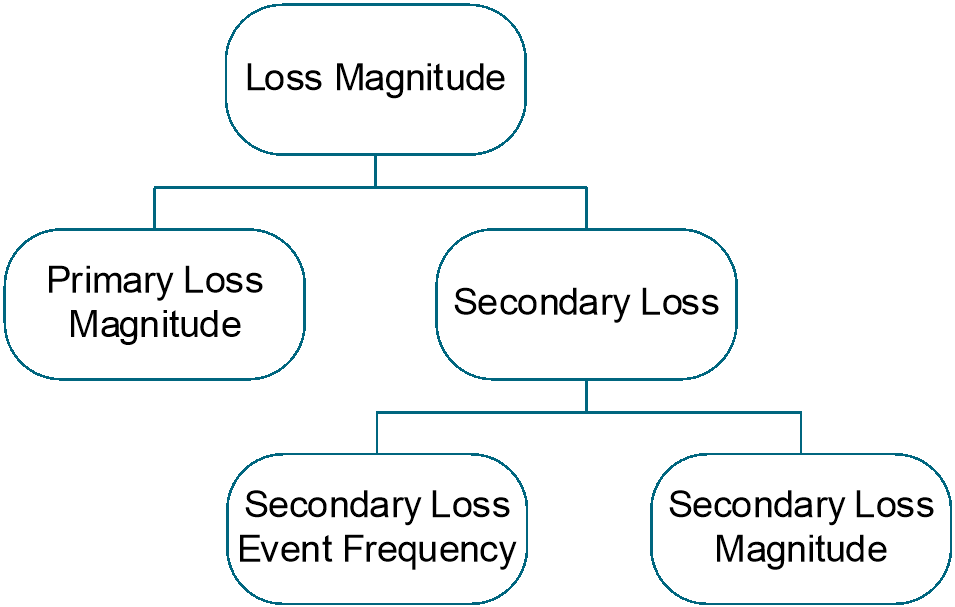
Figure 8: Loss Magnitude

Any of the six Open FAIR loss forms (productivity, response, replacement, fines and judgments, competitive advantage, and reputation) could appear as either a Primary Loss or a Secondary Loss, and the loss forms are modeled as being statistically independent of each other. Experience has shown that productivity and replacement costs are more commonly seen as Primary Losses, whereas fines and judgments, competitive advantage, and reputation damage loss are more commonly seen as Secondary Losses. Response costs are commonly seen as both/either Primary and/or Secondary Losses.

5.3.1 Estimate the Primary Loss Magnitude

The Primary Loss Magnitude (PLM) is the direct consequence of a Loss Event, evaluated as the economic cost directly associated by the observed confidentiality, integrity, or availability loss of the Asset.

In estimating the Primary Loss Magnitude, the analyst estimates what is expected to happen (most likely value) versus best and worst-case (maximum/minimum values). If the analyst chooses to evaluate the worst-case proposition, they must also reflect the (generally) much lower frequency of such an outcome.

In determining which forms of loss (e.g., productivity, replacement, response) may apply to the Primary Loss Magnitude, the analyst should discuss with the organization’s subject matter experts that typically respond to or manage adverse events. This is especially useful for analyzing Loss Events that may have not occurred in the past. These discussions around the types of organizational involvement and loss when a given Loss Event materializes help to ensure that all forms of loss are evaluated and that estimates are accurate while remaining usefully precise.

5.3.2 Estimate the Secondary Loss

If the Primary Loss Event results in reactions from Secondary Stakeholders that cause one or more additional losses for the Primary Stakeholder, there has been Secondary Loss, and the analyst needs to estimate the Secondary Loss Event Frequency (SLEF) and Secondary Loss Magnitude (SLM). To estimate the Secondary Loss, the analyst should first identify who, outside of the organization, has a stake in the compromised information Asset and might react against the Primary Stakeholder to generate additional loss.

After establishing which Secondary Stakeholders are relevant, the analyst should estimate the Secondary Loss Event Frequency.

The next step is to estimate the Secondary Loss Magnitude for each loss form resulting from the reactions of Secondary Stakeholders. These shall be estimated as losses to the Primary Stakeholder, not the impact to Secondary Stakeholders who react from that impact and try to cause a loss to the Primary Stakeholder.

5.3.3 Decomposing Loss Magnitude

Figure 9 shows the decomposition of Loss Magnitude.

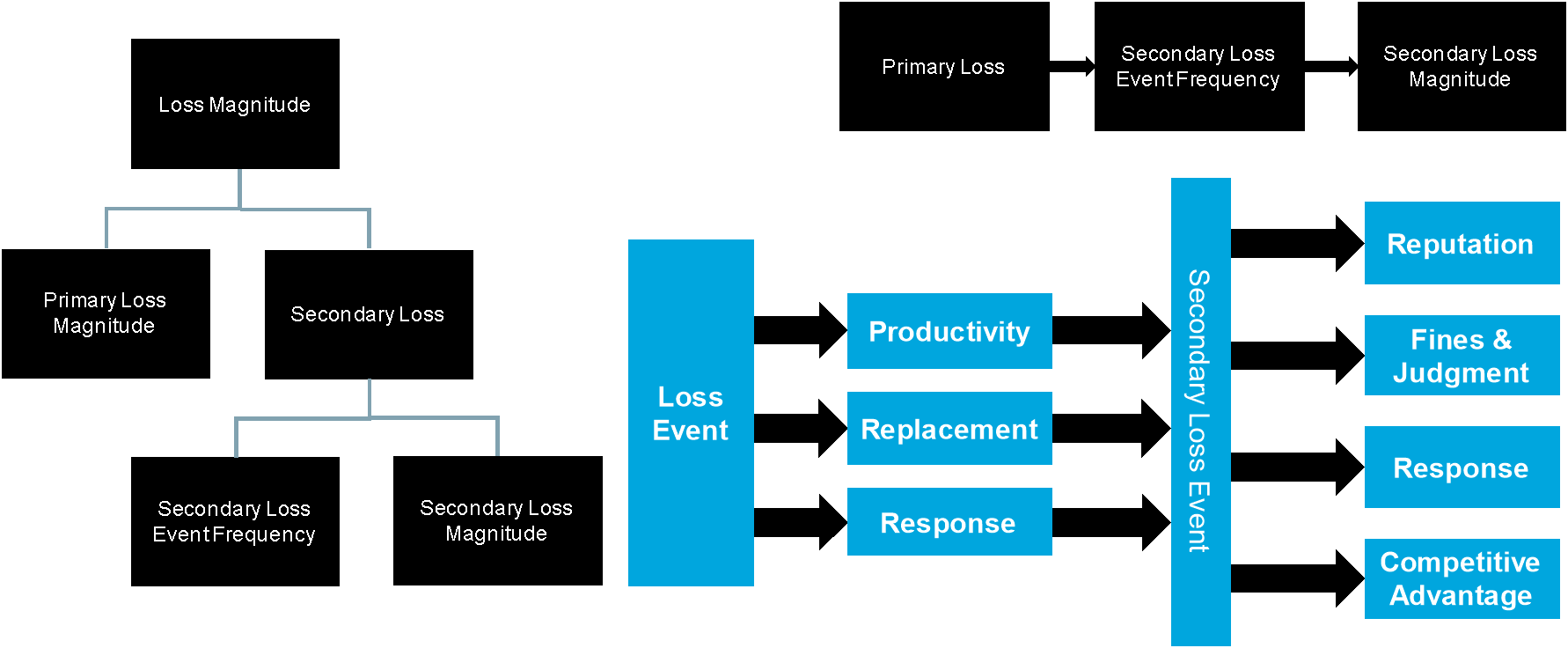
Figure 9: Decomposing Loss Magnitude

Any of the six loss forms can appear as either a Primary Loss or a Secondary Loss, and Loss Magnitude is equal to the sum of the Primary Loss Magnitude and the Secondary Loss Magnitude. Primary Loss Magnitude is the direct consequence of the Primary Loss Event.

For a Secondary Loss to occur, there must have been a Primary Loss that caused Secondary Stakeholders to react and cause additional losses to the Primary Stakeholder. Therefore, the Secondary Loss Event Frequency is the conditional probability that a Primary Loss will result in a Secondary Loss. Secondary Loss Magnitude is the sum of additional losses to the Primary Stakeholder resulting from Secondary Stakeholders’ reactions.

5.4 Stage 4: Derive and Articulate Risk

The analyst now has modeled the two components of risk from the Loss Scenario: the Loss Event Frequency and the Loss Magnitude. From the gathered and/or calibrated estimates of Loss Event Frequency (or its decomposed factors) and Loss Magnitude, the analyst can then derive and articulate risk associated with the described Loss Scenario. To quantitatively estimate the risk, the analyst performs a Monte Carlo analysis of the risk. The direct results of that analysis are the simulated trials of Monte Carlo analysis.

Analysts should provide data that is useful for the decision the stakeholder is trying to make. In other words, analysts must select and present results that are fit for the purpose of the analysis.

Depending upon that purpose, analysts have to decide whether presenting one number that summarizes the distribution of the Monte Carlo results or presenting the distribution itself best serves the stakeholder’s needs.

5.4.1 Single Number Summary Results

Summary results that have shown to be useful include:

• Average – this is the mean of the Monte Carlo simulated results indicating the average of total losses within a given time period (likely a year)
• Most Likely Value – this is the “peak” of the distribution of the simulated results
• Loss Exceedance Result – this is the percentile threshold result

Many times, a stakeholder will want to know the likelihood of a loss exceeding a given threshold; for example, a distribution may indicate that nine times out of ten losses are below $1M, exceeding $1M one time out of ten, so the 90^th percentile threshold is $1M.

• Maximum/Minimum simulated loss – this is the single maximum/minimum simulated loss result

Similar to the loss exceedance result, some stakeholders may find the extremes of the distribution important decision criteria.

There are many single number summaries available beyond those representing risk. Analysts, for example, may choose any of the above to discuss Loss Event Frequency by itself, Single Loss Magnitude, Single Primary Loss Magnitude, Single Secondary Loss Magnitude, etc., depending upon the purpose of the analysis and the decisions stakeholders are making that require analysis to support. Analysts have many choices over what summary information they can provide and need to select the right results as appropriate to the decision that analysis supports.

5.4.2 Characterizing and Presenting Distribution Results

Fundamentally, the results of a risk analysis are the distribution of the Monte Carlo analyses of total annual losses, the number of Loss Events per year, the single total loss, single Primary Loss, and single Secondary Loss. A distribution can be expressed in many ways, and analysts need to choose that expression as best serves the purpose of the analysis. Example presentations include:

• Loss exceedance curve
• Distribution curve
• Tornado chart[4] (if comparing various alternatives)

5.5 Stage 5: Model the Effect of Controls

The analyst can now estimate the effects of mitigating the risk described by the Loss Scenario through changes in Controls. The Open FAIR framework defines four categories of Controls: avoidance, deterrent, vulnerability, and responsive. These Controls affect specific Open FAIR factors, but their overall effect is to reduce either the likelihood of a Loss Event, the effect of Loss Prevention Controls, or to mitigate losses once a Loss Event has begun to occur, the effect of Loss Mitigation Controls.

5.5.1 Open FAIR Control Categories

All Controls are intended to affect either or both the frequency and magnitude of loss; thus, a workable definition of Control is any person, policy, process, or technology that has the potential to reduce the frequency and/or magnitude of future loss. Understanding where a Control’s effect may be realized within the Open FAIR taxonomy is critical to accurately account for a Control within an analysis.

At a basic level, the Open FAIR model categorizes Controls by how they affect risk:

1. Avoidance Controls affect the frequency and/or probability of Threat Agents establishing contact with Assets.

2. Deterrent Controls affect the probability that a Contact Event becomes a Threat Event.
3. Vulnerability Controls affect the probability that a Threat Event will result in a Loss Event (the probability that Threat Capability will overcome Resistance Strength), usually by changing the Asset’s Resistance Strength.
4. Responsive Controls affect the Loss Magnitude, either by limiting Primary Losses, limiting the frequency of Secondary Loss Events, or limiting the magnitude of Secondary Loss Events.

Note: The Open FAIR model does not include a specific “detective control” category because detective controls can play a role in each of the categories listed above and thus is not a distinct Control category. For example, system logging and monitoring can in some circumstances be a deterrent by increasing a potential Threat Agent’s perception of the likelihood of being caught. At the same time, logging and monitoring can inform an organization that an event is underway, allowing it to intervene before loss materializes. Even if intervention is not timely enough to prevent loss from occurring, early detection can allow an organization to respond quickly enough to minimize the magnitude of loss.

Figure 10 identifies where these Control categories play a role within the taxonomy.

Figure 10: Control Categories

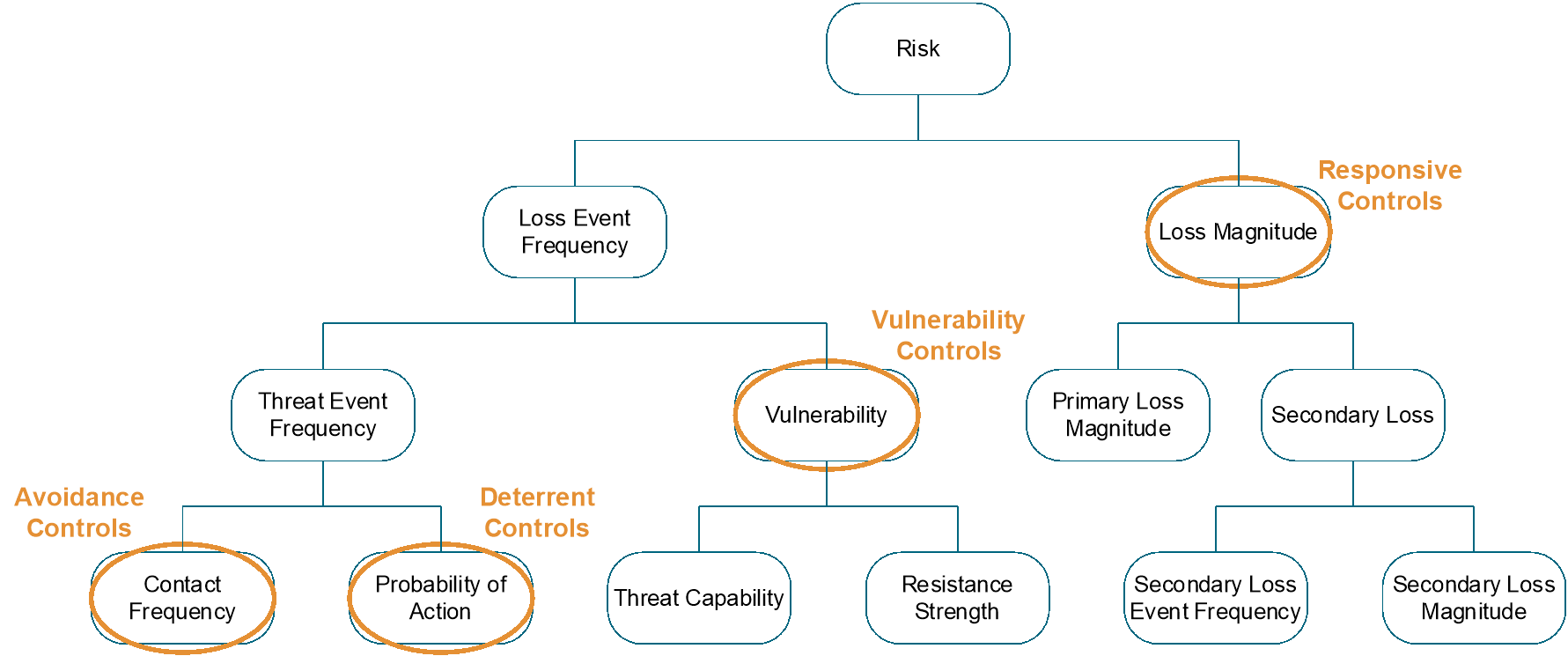
5.5.1.1    Avoidance Controls

Avoidance Controls affect the frequency and/or likelihood that a Threat Agent will come into contact with an Asset. An Avoidance Control successfully reducing Contact Frequency will translate into a lower Threat Event Frequency, causing a reduced Loss Event Frequency, and lessened exposure to risk. In other words, Avoidance Controls limit the Threat Agent’s ability to contact the Asset in the first place. Therefore, Avoidance Controls are a Loss Prevention Control.

Examples of information security-related Avoidance Controls include:

• Firewall filters
• Physical barriers
• The relocation of Assets
• The reduction of threat populations (e.g., reducing the number of personnel who are given legitimate access to Assets)

As with any control, the effect may not be absolute. For example, firewalls usually are configured to permit certain types of traffic, which means that Threat Events may still occur against Assets behind the firewall. Nonetheless, firewalls also almost invariably reduce the frequency of Threat Events by shielding against certain types of traffic.

When considering the effect of Avoidance Controls in an analysis, the analyst can measure or estimate the reduction in Contact Frequency specific to the Threat Agent/Community under consideration.

5.5.1.2    Deterrent Controls

Deterrent Controls reduce the probability that a Threat Agent will act against the Asset in a manner that may result in loss – the Probability of Action. In other words, Deterrent Controls are designed to make it less probable that, given a Contact Event, the Threat Agent will launch a Threat Event. As with Avoidance Controls, this effect flows up the taxonomy to affect Threat Event Frequency, Loss Event Frequency, and exposure to risk. Therefore, Deterrent Controls are also a Loss Prevention Control.

Examples of common information security-related deterrent controls include:

• Policies
• Logging and monitoring
• Enforcement practices
• Asset “hardening” (i.e., many threat actors are opportunistic in nature and will gravitate toward easier targets, rather than targets that are perceived to be difficult)
• Physical obstacles (e.g., external lights on a building, barb-wire fencing)

For a Deterrent Control to impact the Threat Agent’s Probability of Action, the Threat Agent must be aware of the Control. Deterrent Controls are designed to impact the Threat Agent’s perceived risk in carrying out the Threat Event, perceived level of effort required to impact the Asset in the desired way, and/or perceived risk of being caught/punished/harmed. Human Threat Agents may be deterred in this way while non-human threat actors may not.

Measuring the effect of Deterrent Controls is often challenging. Nonetheless, reasonable, calibrated estimates can be made to reflect their value.

5.5.1.3    Vulnerability Controls

Vulnerability Controls reduce the probability that a Threat Agent’s action will result in a Loss Event. In a scenario where the context is a malicious action, Vulnerability Controls generally focus on increasing the difficulty a Threat Agent faces in their attempts to breach or otherwise impair an Asset. In a scenario where the context is non-malicious (e.g., human error), Vulnerability Controls often focus on reducing complexity and/or difficulty faced by personnel to reduce the probability that their actions will result in harm. In other words, Vulnerability Controls improve the Resistance Strength of the Asset. Vulnerability Controls are also a Loss Prevention Control.

Note: Vulnerability Controls are sometimes referred to as “resistive controls”, but this term tends to exclusively connote controls against malicious acts.

Examples of Vulnerability Controls in an information security context would include:

• Authentication
• Access privileges
• Patching
• Some configuration settings

The effects of Vulnerability Controls are reflected in estimates of either Resistance Strength or Vulnerability, depending on the level of abstraction of the analysis.

5.5.1.4    Responsive Controls

Responsive Controls are designed to reduce the magnitude of loss that results from a Loss Event. Therefore, Responsive Controls are a Loss Mitigation Control.

Examples of response controls in an information security context include:

• Backup and restore media and processes
• Forensics capabilities
• Incident response processes
• Credit monitoring for persons whose private information has been compromised

Measurements and estimates regarding the effect of Responsive Controls are applied in the Loss Magnitude branch of the taxonomy and are reflected as lower monetary Loss Magnitudes.

In closing, for a control to affect risk, it must affect one or more risk factors defined in the Open FAIR taxonomy. Analysts must evaluate all applicable current-state controls and their overall effectiveness. Data on these is often available by reviewing the following:

• Audits (technical and regulatory) – audits that evaluate the effectiveness of controls can provide useful information about the current state and possibly an indication of the continued state of controls
• Penetration Tests/Security Scans – these exercises can provide useful knowledge of where controls are present and how effective they may be in preventing a threat action from materializing into a loss

Some penetration tests also provide good insight into the overall responsiveness of the organization (with regard to identifying threat actions).

5.5.2 Mapping Open FAIR Controls to the NIST Cybersecurity Framework

The Open FAIR control categories map well to other industry standard methods of categorizing and conceptualizing security functions. The NIST Cybersecurity Framework (CSF), for example, defines five functions:[5] Identify, Protect, Detect, Respond, and Recover. These five functions are frequently implemented through physical, administrative, and technical security controls.

Figure 11: NIST CSF Five Functions

The Open FAIR Avoidance, Deterrent, and Vulnerability Control categories all map to the Protect function, the function that prevents losses from occurring in the first place.

The Open FAIR Responsive Control category spans across the Detect, Respond, and Recover functions, those functions that take place once a loss begins to occur.

Security practitioners can categorize controls to the NIST CSF five functions to map how Controls affect risk.

5.6 Putting It All Together

The previous sections demonstrate a method for analyzing risk. By defining a Loss Scenario, modeling the risk associated with it using the Open FAIR taxonomy, and gathering estimates for the factors of the model while considering the specific impacts controls have on those factors, an analyst can generate probabilistic forecasts of future loss.

While the analyst is responsible for helping the organization understand “How much risk do we have?”, risk managers and decision-makers must answer different questions: “How does current-state risk compare to tolerance, and what, if anything, should be done to reduce probable future loss from a given Loss Scenario?”.

Doing something about risk consists of implementing controls that either reduce the Loss Event Frequency (prevent the Loss Scenario from occurring as often) or reduce the Loss Magnitude of the Loss Event once it has occurred (mitigate the severity of the loss). Analysts model the effects of these controls by how they affect one or more of the Open FAIR risk factors.

Figure 12 combines the decomposition of the Loss Scenario with the Open FAIR Controls and Categories as well as the NIST CSF color scheme.

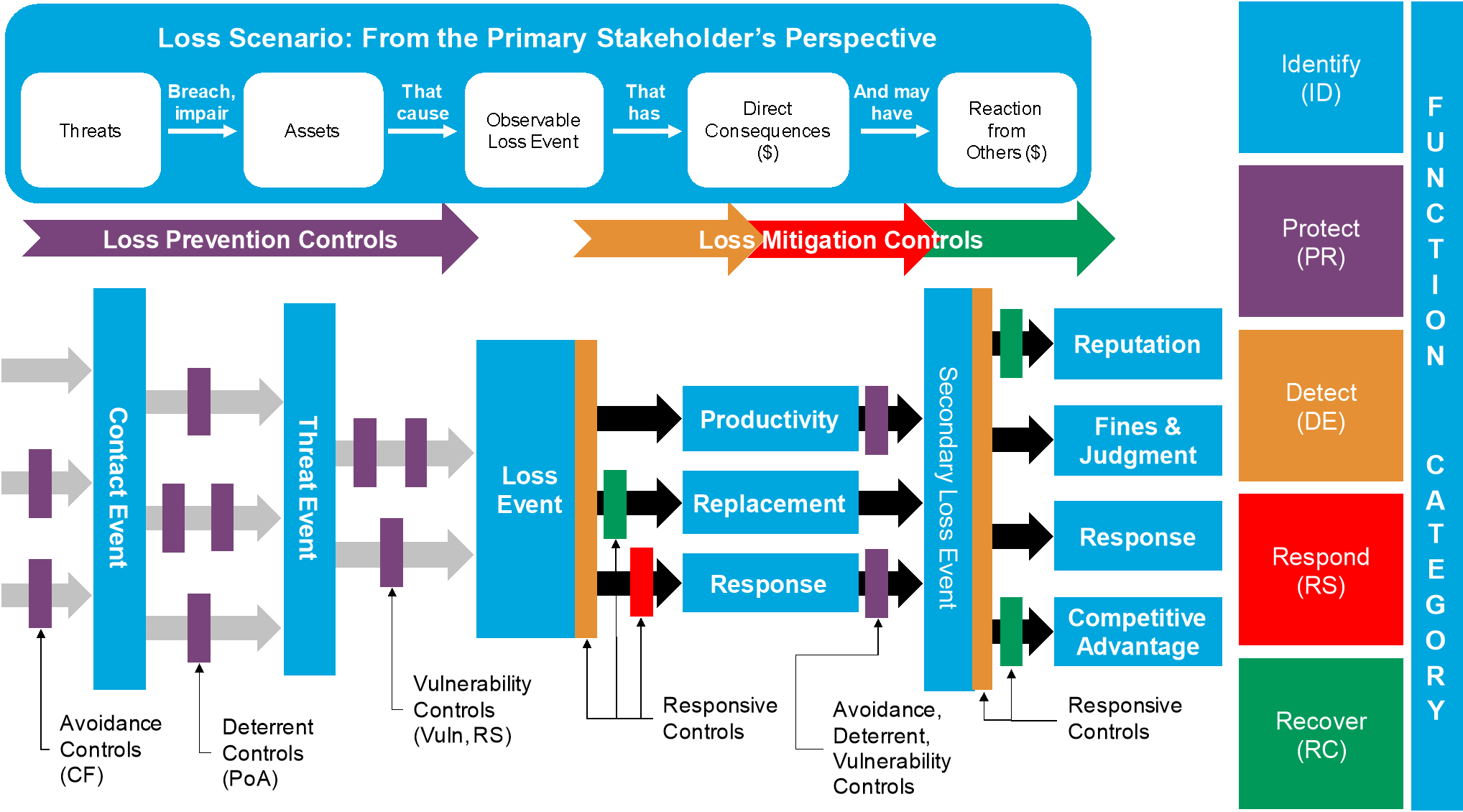
Figure 12: Decomposing an Open FAIR Loss Scenario, including the Open FAIR Control Categories and the NIST CSF Five Functions

6.1 Documenting Assumptions and Rationale

When performing an Open FAIR analysis, the estimates are often only as good as the assumptions and rationale documented along with them. When performing a risk analysis, the analyst should anticipate that aspects of it might be challenged, especially from stakeholders who have other assumptions or biases. The assumptions and rationale need to clearly and concisely define, and must support, any estimates used.

Recall that well-documented assumptions should include the reasoning for the assumption as well as any sources that contributed to them. Well-documented rationale should state the source of all estimates. The source may be systems (e.g., logs), groups (e.g., incident response), or industry data.

Good sources of data are ones which are more objective in nature than subjective. Objective data is often more defensible and credible than opinion-based data. While any analyst would prefer objective-based estimates, sometimes good data is missing. When a situation like this arises, it is not the time to try and “hide” it by poorly documenting the rationale; instead, a credible analyst should document the missing data and the rationale for what was assumed instead/in addition.

6.2 Diminishing Returns

There are diminishing returns to gathering more data, investigating more data, and drilling deeper into the Open FAIR taxonomy.

Douglas Hubbard (see Referenced Documents) suggests that:

“The information value curve is usually steepest in the beginning. The first 100 samples reduce uncertainty much more than the second 100.”

To the risk analyst, this means that there is a diminishing return associated with gathering more data to support a single model or risk factor estimate. Deeper investigation of a risk factor can come at an increased cost to the analyst, and the analyst should be aware of this cost/benefit tradeoff.

There is also a diminishing return to estimating lower levels of the Open FAIR taxonomy. Risk analysts should estimate the risk factors that have the highest quality of data to support accurate and usefully precise analyses. When possible, analysts should estimate factors at the highest levels of the Open FAIR taxonomy. However, when an accurate estimate is not usefully precise and information is available that informs accurate and usefully precise estimates of lower-level risk factors, the analyst should decompose the higher-level risk factor into its component sub-factors and estimate them.

6.3 Capacity and Tolerance for Loss

An organization’s capacity for loss can be interpreted as an objective measure of how much damage it can incur and still remain solvent. For many organizations, this is a function of its capital reserves and other tangible resources, as well as its position in the market. For example, an organization with a large inventory of raw materials has a greater capacity to absorb a disruption in its supply chain than one that operates on just-in-time delivery of raw materials.

Although an organization may have a high capacity for loss, its management team may not allow the organization to expose itself to a loss exceeding a substantially lower threshold than the capacity for loss. That subjective preference and management mandate is the tolerance for loss. Although there often is a strong correlation between the (objective) capacity for loss and the (subjective) tolerance for loss, there can be significant differences if executive management is personally loss averse. For example, a financial institution may have substantial reserves and a resilient market presence, yet it may act highly averse to loss for management’s personal business practice, customer demands, market norm, or regulatory reasons.

Ultimately, it is the combination of capacity for loss and tolerance for loss that determines how an organization perceives and responds to risk.

6.4 Risk Qualifiers

Sometimes, quantitative results do not communicate everything that may be necessary for well-informed decisions to be made. Within the Open FAIR framework, there are two qualifiers that can help decision-makers understand subtle considerations not reflected in numeric data: the Fragile qualifier, and the Unstable qualifier.

The Fragile qualifier is used to represent conditions where the Loss Event Frequency is low in spite of a high Threat Event Frequency, but only because a single preventative Control exists. In other words, while the level of risk is low, it is qualified as fragile because the low risk level is based on a single point of failure. For example, if a single control were all that kept malware-related losses low, then that could be said to be a fragile condition.

The Unstable qualifier is used to represent conditions where the Loss Event Frequency is low solely because Threat Event Frequency is low. In other words, no preventative controls exist to mitigate the frequency of Loss Events. An example might be the risk associated with rogue database administrators. For most organizations, this is a low Loss Event Frequency condition but only because it is an inherently low Threat Event Frequency scenario. Should the Threat Community conditions change, Loss Event Frequency rises due to the absence of any effective Vulnerability Control.

These qualifiers are intended to compensate for the fact that in some scenarios, if a decision-maker only looked at the low Loss Event Frequency, they may be lulled into a sense of security that is not warranted.

6.5 Using Ordinal Scales for Analysis

Ordinal data is a categorical, statistical data type where the variables have natural, ordered categories and the distances between the categories is not known. Using ordinal scales (e.g., 0-5 or high, medium, and low) to measure components in a risk analysis, or to categorize overall risk level, can bring numerous problems:

• Frequently, the meaning of each ordinal value does not carry a tangible, economic meaning to it; for example, an ordinal scale of 5 meaning “severe” can mean different things to different people
• Even if ordinal values represent well-defined ranges, they let analysts represent ranges that span multiple ordinal values; for example, if an ordinal scale starts at 1, defined as a range of probability from 1-20%, and the ordinal scale 2 is defined as 21-40%, how does an analyst deal with a range of probability from 15-35%?
• Ordinal numbers cannot validly be used as inputs into mathematical formulas because they are not ratio values; a “5” is most likely not five times more severe than a “1”

Math combining ordinal values representing Loss Event Frequency and others representing Loss Magnitude are especially problematic to combine and get meaningful results.

6.6 Translating Quantitative Results into Qualitative Statements

One of the advantages to quantitative risk analysis is that numbers are dispassionate and, by themselves, neutral to bias. Of course, decision-makers may not want to take the time to personally interpret the significance of quantitative results and would prefer a simple red, yellow, or green label to look at. Fortunately, it can be relatively simple to translate numeric values to qualitative statements.

These translations should be guided by scales that have been approved by management.

It is inappropriate for risk analysts to define and use qualitative scales that represent their tolerance for loss or their personal interpretation of what they believe to be the organization’s tolerance for loss. The challenge, of course, is that management may not be readily available to formally define risk scales. In this circumstance, the analyst may define a scale they believe is accurate for the organization and then have the scale reviewed by management for approval.

Table 1: An Example Scale Translating Quantitative Values to Qualitative Labels

Label	Average Annualized Loss Exposure
Severe (SV)	> $10,000,000
High (H)	$1,000,000 to $9,999,999
Moderate (M)	$100,000 to $999,999
Low (L)	$10,000 to $99,999
Very Low (VL)	< $10,000

Using the example scale shown in Table 1, if an analysis resulted in an average annualized loss exposure of $4.5M, that could be interpreted as high risk.

Note:  Using a qualitative scale to present quantitative results can be misleading. Fragile or unstable qualifiers do not translate into qualitative statements. Moreover, results presented qualitatively do not include the ranges used to estimate the quantitative results. Finally, as described in the previous section, using ordinal scales – even when well-defined – neglects the nuances that quantitative results include.

6.7 Troubleshooting

When analysts or stakeholders disagree on the results of or a component of an analysis, there are three recommended techniques to managing the disagreements.

The first technique is to revisit the scoping or rationale within an analysis and determine whether an assumption has been made which varies from the other analysts or stakeholders. If a difference is found, this is often easily resolved. If rationale/assumptions are not documented, the risk analyst cannot troubleshoot or defend their analysis if there are disagreements.

The second technique is to leverage the Open FAIR taxonomy. The taxonomy breaks down the factors that drive risk. For example, if a disagreement exists regarding estimates made at the Loss Event Frequency level, stepping down to a lower level of abstraction may allow both sides to find agreement, and the higher estimate will now be derived.

The third recommended technique is to perform two or more analyses to encompass the disagreement. As an example, if one analyst believes the Threat Event Frequency is at least once a year while a second analyst believes the Threat Event Frequency is less frequent, they can perform analyses using both figures and observe whether there is a significant deviation in the overall results.

Often, the majority of disagreements will be resolved after approaching the problem using the first two techniques.

A.1     Risk Management Decision-Making

Risk management is fundamentally about making decisions – decisions about which risk issues are most critical (prioritization), which risk issues are not worth worrying about (risk acceptance), and how much to spend on the risk issues that need to be dealt with (budgeting). In order to be consistently effective in making these decisions, we need to be able to compare the issues themselves, as well as the options and solutions that are available. In order to compare, we need to measure, and measurement is predicated upon a solid definition of the things to be measured. Figure 13 shows these chained dependencies.

Figure 13: Chained Dependencies

To date, the information security profession has been hamstrung by several challenges, the least of which is inconsistent nomenclature. For example, in some references, software flaws/faults that could be exploited will be called a “threat”, while in other references these same software faults will be referred to as a “risk”, and yet other references will refer to them as “vulnerabilities”. Besides the confusion that can result, this inconsistency makes it difficult if not impossible to normalize data and develop good metrics.

A related challenge stems from mathematical equations for risk that are either incomplete or illogical. For example, one commonly cited equation for risk states that:

Risk = (Threat * Vulnerability) / Controls

Amongst other problems, this equation does not tell us whether Threat means the level of force being applied or the frequency with which threat events occur. Furthermore, impact (magnitude of loss) is left out of the equation altogether. As we will touch on shortly, organization management cares very deeply about the question of Loss Magnitude, and so any risk equation that ignores impact is going to be meaningless to the very people who need to use risk analyses to make risk decisions.

These issues have been a major contributor to why the information security profession has consistently been challenged to find and maintain “a seat at the table” with the other organizational functions (e.g., finance, marketing). Furthermore, while few people are likely to become excited with the prospect of yet another set of definitions amongst the many that already exist, the capabilities that result from a well-designed foundational taxonomy are significant.

Likewise, in order for our profession to evolve significantly, it is imperative that we operate with a common, logical, and effective understanding of our fundamental problem space. The O-RT Standard seeks to fill the current void and set the stage for the security profession’s maturation and growth.

Note: Any attempt to describe the natural world is destined to be incomplete and imprecise to some degree due to the simple fact that human understanding of the world is, and always will be, limited. Furthermore, the act of breaking down and categorizing a complex problem requires that black and white lines be drawn where, in reality, the world tends to be shades of gray. Nonetheless, this is exactly what human-critical analysis methods and science have done for millennia, resulting in a vastly improved ability to understand the world around us, evolve, and accomplish objectives previously believed to be unattainable.

This document is a current effort at providing the foundational understanding that is necessary for similar evolution and accomplishment in managing information risk. Without this foundation, our profession will continue to rely too heavily on practitioner intuition which, although critically important, is often strongly affected by bias, myth, and commercial or personal agenda.

[1] Merriam Webster: https://www.merriam-webster.com/.

[2] Poisson distribution: https://en.wikipedia.org/wiki/Poisson_distribution.

[3] Monte Carlo method: https://en.wikipedia.org/wiki/Monte_Carlo_method.

[4] Tornado chart: https://en.wikipedia.org/wiki/Tornado_diagram.

[5] NIST CSF five functions: https://www.nist.gov/cyberframework/online-learning/five-functions.